konsultacja matematofil: Cięciwa paraboli o równaniu y = −a²x² + 5ax − 4 jest styczna do krzywej y = 1/1−x w punkcie P (2, −1), który dzieli tę cięciwę na połowy. Znaleźć wartość parametru a. f ' (x)=1/(1−x²) a= f ' (x_o) czyli −a²=1/(1−2)²?

Blee:

	1
g(x) =
	1−x

	1
g'(x) = −
	(1−x)2

g'(2) = −1 = a' (to nie jest to 'a' o które chodzi w zadaniu) cięciwa dana jest więc wzorem: h(x) = a' * x + b −> h(x) = −x + b ....−1 = −2 + b −> b = 1 h(x) = −x + 1 <−−− wzór cięciwy teraz wiemy, że cięciwa posiada środek w puncie P( 2 , −1 ) i teraz musimy zobaczyć dla jakiego współczynnika 'a' (w tej paraboli) zajdzie to co jest podane w zadaniu (cięciwa o równaniu y = −x + 1 jest dzielona na pół w punkcie P(2, −1) )

matematofil: Czy przed pochodną powinien być "−"? według mnie h(x) = x − 3 nie wiem jak mam to sprawdzić

Blee: masz rację ... nie powinno być minusa

Blee: h(x) = x − 3 h(x) = f(x) ⇔ a²x² + (1 − 5a)x + 1 = 0 powyższe równanie musi mieć DWA różne rozwiązania więc warunek 1 −−− Δ > 0 Δ = (1−5a)² − 4a² = 21a² − 10a + 1 > 0 teraz −−− zauważ, że skoro punkt P(2,−1) ma dzielić cięciwę na pół, to znaczy, że: istnieje takie x₀, że: h(2 − x₀) = f( 2 − x_o) ∧ h(2 + x₀) = f(2 + x_o) czyli:

⎧	a2(2 − x0)2 + (1 − 5a)(2 − x0) + 1 = 0
⎩	a2(2 + x0)2 + (1 − 5a)(2 + x0) + 1 = 0

a²[ (2 − x₀)² − (2 + x₀)² ] + (1−5a)*[ (2 − x₀) − (2 + x₀)] = 0 a²* [(2−x₀) + (2+x₀)]*[(2−x₀) − (2+x₀)] − (1−5a)*2x₀ = 0 8a²x₀ + 2(1−5a)x₀ = 0 oczywiście rozpatrujemy sytuację dla x₀ ≠ 0 4a² − 5a + 1 = 0 (−4a + 1)(−a + 1) = 0 −> a = −1 lub a = −1/4

Blee: i coś popitoliłem

Blee: oczywiście na końcu: a = +1 lub a = +1/4

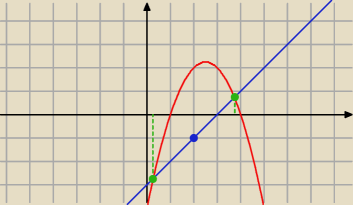
Blee: sprawdzenie: f(x) = −x² + 5x − 4 = −(x−4)(x−1) przynajmniej na pierwszy rzut oka wygląda dobrze (trza policzyć)

Blee: sprawdzenie a = 1/4 pokazuje −− że coś nadal jest nie tak ... sprawdzaj co zrobiłem i szukaj błędu

Blee: już widzę: Δ = 21a² − 10a + 1 > 0 ⇔ a ∉ <1/7 ; 1/3> dlatego a = 1/4 odpada

matematofil: Dziękuje za pomoc z zadaniem ale mam pytanie, co znaczy ta linijka h(x) = f(x) ⇔ a²x² + (1 − 5a)x + 1 = 0

Blee: h(x) = f(x) <−−−− to równanie spełniają punkty przecięcia się prostej h(x) i paraboli f(x) czyli tą są punkty 'początku' i 'końca' tejże cięciwy (która leży na prostej h(x) )

matematofil: Mhm rozumiem już a jeszcze jakbym mógł spytać to skąd b=(1−5a) oraz wgl jak mam wpasc na takie równanie?

Blee: h(x) = x − 3 = −a²x² + 5ax − 4 = f(x) x − 3 + a²x² − 5ax + 4 = 0 a²x² + (1−5a)x + 4 = 0 <−−− stąd jak masz wpaść na równanie h(x) = f(x) yyyyyyy ... no musisz sprawdzić kiedy w ogóle może istnieć cięciwa (leżąca na prostej h(x) ) dla paraboli f(x) nie wiem jak Ci inaczej odpowiedzieć na to pytanie −−− to tak jakbyś się mnie zapytał po co w zadaniu: "dla jakiej wartości parametru 'a' równanie kwadratowej x² − ax + 5 = 0 ma jedno rozwiązanie" byś się mnie pytał po co liczy się Δ i jak masz na to wpaść.