Zadanie z rachunku różniczkowego MateuszS: Dana jest parabola o równaniu y=x²+bx+c. Prosta o równaniu 5x−y+1=0 jest styczna w punkcie A, a prosta o równaniu x+y+8=0 jest do niej styczna w punkcie B. Oblicz pole trójkąta ABC, w którym punkt c jest wierzchołkiem paraboli.

Bleee: W jaki sposób można wyznaczyć współczynnik kierunkowy stycznej (w danym punkcie) do krzywej mając wzór danej krzywej?

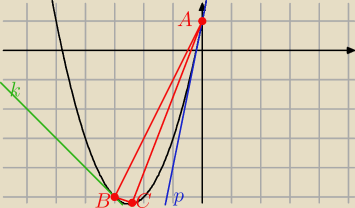
a@b: 1/ Rozwiąż układy równań prostej p i paraboli oraz prostej k i paraboli przyrównaj Δ=0 otrzymasz b=5 i c=1 i masz równanie paraboli y= x²+5x+1 C=W=(−5/2; −21/4) f^'(x) = 2x+5 f^'(x_o)= 5 ⇒ x_o=0 to y_o=1 A(0,1) f^'(x_o)= −1 ⇒ x_o=−3 to y_o= −5 B(−3,−5) P(ABC)= ............... P=15/8 ========