matematykaszkolna.pl
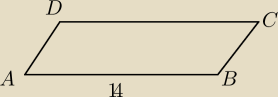
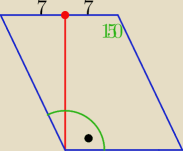
planimetria salamandra: rysunekDługośc jednego z boków równoległoboku jest równa 14. Wysokość równoległoboku poprowadzona z wierzchołka na ten bok dzieli go na połowy. Jeden z kątów równoległoboku ma miarę α. Oblicz pole P i obwód L równoległoboku, gdy α=45, α=60, α=150 Nie rozumiem zbytnio treści, tj. jak wykonać rysunek, dalej sobie poradzę. Nie wiem gdzie tę wysokość zaznaczyć.
17 lut 22:18
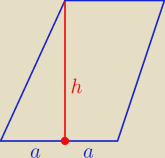
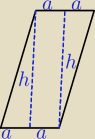a@b: rysunek
17 lut 22:20
a@b: zamiast a a wpisz na rys : 7 7
17 lut 22:23
salamandra: Jasne, o to chodziło, dzięki
17 lut 22:27
salamandra: rysunekRozumiem, że działa to również w tę stronę?
17 lut 22:29
a@b: dokładnie emotka
17 lut 22:30
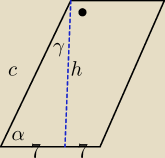salamandra: rysunekjednak mam problem w c) α=150, w dwóch pierwszych przypadkach zakładałem tak jak na rysunku, ale teraz muszę założyć, że to kąt rozwarty, więc tam przy kącie prostym na górze? więc γ= 150−90= 60 i z tego liczyć?
17 lut 22:38
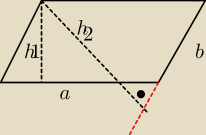
a@b: rysunek
17 lut 22:41
salamandra: tak myślałem emotka
17 lut 22:43
a@b: emotka
17 lut 22:53
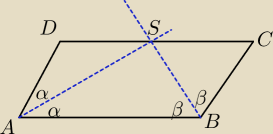salamandra: rysuneka na to istnieje jakiś prostszy sposób? W równoległoboku ABCD wysokość h1=2 i h2= 4 Obwód L ma dlugosc 48. Oblicz dlugosc boków a i b. P=a*h 48=a*2 48=b*4 2a=4b a=2b L=2a+2b 48=4b+2b 48=6b b=8 a=16
17 lut 22:57
a@b: ok
17 lut 23:01
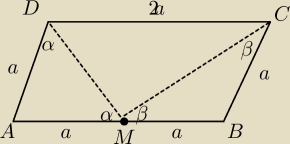salamandra: rysunekUzasadnij, że dwusieczne dwóch sąsiednich kątów równoległoboku sa prostopadłe 2α+2β=180 α+β=90 stąd kąt ASB = 90, i tyle?
17 lut 23:07
a@b: tak
17 lut 23:07
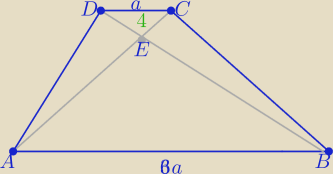salamandra: rysunekW równoległoboku ABCD, w którym bok AB jest dwa razy dłuższy niż bok BC połączono środek M boku AB z wierzchołkami C i D. Wykaż, że kąt CMD ma miarę 90 stopni. Tu już trochę mi brakuje pomyslu
17 lut 23:12
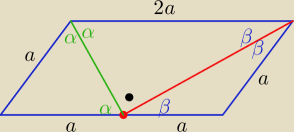a@b: rysunek P(DCE)=4 , |AB|=6a , |DC|=a Oblicz pole trapezu i zakoduj trzy pierwsze cyfry otrzymanego wyniku | | | |
17 lut 23:14
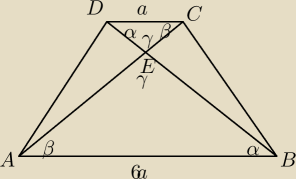a@b: rysunek 2α+2β=............
17 lut 23:18
a@b: Żyjesz?
17 lut 23:25
salamandra: rysunekTrójkąty ABE i DCE podobne na mocy cechy kk.
AB DE 
=
DC EB 
 DE 
6=
 EB 
6|DE|= EB niech DE= x EB=6x CE=y AE=6y PΔDCE = x*y*sinγ
 1 
4=
*x*y*sinγ / * 2
 2 
8=x*y*sinγ
 1 
PΔAEB =
*6x*6y*sinγ
 2 
2PΔAEB =6x*6y*sinγ = 36(x*y*sinγ) PΔAEB= 36*4 = 144
17 lut 23:25
salamandra: A dobra, nieważne, pole trapezu miałem policzyć a nie tego trójkąta
17 lut 23:26
salamandra: 23:18 intuicje miałem dobrą, ale odwagi zabrakło, by jeszcze ten naprzemianległy dopisac i coś kombinować z tego
17 lut 23:27
a@b: Nie! P=(k+1)2*P(DEC) , k = −−−− ( skala podobieństwa trójkątów (których? ....... |1|9|6|
17 lut 23:28
salamandra: Ja policzyłem tylko trójkąta AEB, nie policzyłem całego trapezu.
17 lut 23:29
a@b: Masz wzór więc "szast−prast" i po ptokach ! ( szkoda czasu ..... za marne 2pkt emotka
17 lut 23:32
salamandra: Ale mając tę podstawkę co zrobiłem.
 1 
PΔAED =
*DE*AE*sin(180−γ) =
 2 
 1 1 
=
*x*6y*sinγ =
*6(x*y*sinγ)= 6*4=24
 2 2 
PΔECB = 24 P trapezu= 24+24+144+4 = 196
17 lut 23:36
a@b: ok
17 lut 23:37
salamandra: A skąd ten wzór z 23:28?
17 lut 23:38
a@b: Wpisz w forumową wyszukiwarkę "Eta trapez" Zobaczysz ile razy już ten wzór wyprowadzałam emotka
17 lut 23:43
salamandra: Jutro zerknę emotka w ogóle to zadanie z jakiejś matury podstawowej/rozszerzonej?
17 lut 23:46