styczna jaros: Jakieś pomysły? Napisać równanie okręgu stycznego do dwóch prostych równoległych y = x − 4 i y = x − 12, jeżeli jego środek leży na prostej y = −x.

salamandra: odległość dwóch prostych wyznaczy ci średnicę.

jaros: ale to z rysunku wyliczasz czy jak?

jc: Środek y=x−8, prosta w połowie pomiędzy dwiema równoległymi przecięcie y=−x y=−4, x=4 promień = 4/√2=2√2

salamandra: Bierzemy dowolny punkt na prostej y=x−4 np. A=(1,−3) d− wzór na odleglosc prostej od punktu

	|Ax0+Bx0+C|
d=
	√A2+B2

w tym szczególnym przypadku, z racji tego, że te proste są równoległe, można zastosować wzór d=

	|C1−C2|
		=
	√A2+B2

	|1*1+(−1)*(−3)−12|		|4−12|		8		8√2
d=		=		=		=		= 4√2
	√12+(−1)2		√2		√2		2

r= 2√2

jaros: Mógłbyś napisać co jest C1 a co C2?

salamandra: x−y−4 oraz x−y−12

jaros: rozumiem, że promień wychodzi r=2√2 ale co z x i y do równania okręgu?

jaros: (x−4)² + (y+4)²=8?

jc: Tak.

jaros: A ja moge tak po prostu zauważyć, że środek okręgu miedzy prostymi będzie na danej prostej?

Bleee: Jeżeli masz dwie proste ROWNOLEGLE to wtedy wiesz ze środek jest gdzies na prostej 'posrodku' tych prostych. Gdyby proste nie były równolegle Wtedy jest troszeczkę więcej zabawy z wyznaczeniem prostej na której będzie leżał środek okręgu (ale niewiele więcej)

jaros: Co w takim przyadku się robi, gdy proste nie są równoległe ?

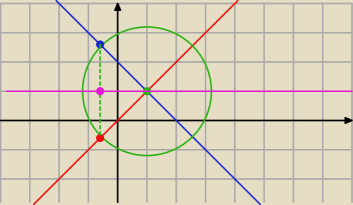
Blee: Jeśli nadal jesteś zainteresowany, to: w momencie gdy dwie proste NIE SĄ równoległe to: 1) w pewnym punkcie się przecinają (wyznaczasz ten punkt) 2) wzór okręgu o dowolnym promieniu i o środku w punkcie przecięcia ( (1) ) 3) wyznaczasz wyznaczasz punkty przecięcia się okręgu z prostymi 4) wyznaczasz środek odcinka łączącego te dwa punkty 5) prowadzisz prostą przechodzącą przez punkty (1) i (4) Uwaga zauważ, że w tym przypadku wyjść DWIE proste (druga będzie w pionie nie zaznaczałem jej, aby nie mieszać wszystkiego na rysunku)