planimetria salamandra: Szybkie pytanie odnośnie równoległoboku. Czy przekątna (jedna) dzieli równoległobok na dwa przystające trójkąty? Mam dylemat czy ten kąt β zostanie podzielony na równe części i w jednym i w drugim trójkącie

janek191: tak

salamandra: Czyli przekątne w równoległoboku to jednocześnie dwusieczne?

Jerzy: Dwa identyczne trójkąty są przystające. O jaki kąt β pytasz ?

Leszek: Nie , tylko w rombie przekatne sa dwusiecznymi !

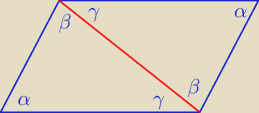
janek191:

salamandra:

Jerzy: @Janek.Jeśli kąt β,to kąt rozwarty,to co ty wygadujesz ?

salamandra: No właśnie mi się przypomniało janek, że chyba już kiedyś mi identyczny rysunek przytaczałeś dzięki

PW: Trójkąty są przystające na zasadzie "bok − kąt α − bok". Kąt β jest dzielony przez przekątną na dwa różne kąty, te kąty są parami równe na zasadzie kątów naprzemianległych.

salamandra: Akurat zadanie mam łatwe− obliczyć pole równoległoboku, w którym boki mają dlugosc 8 i 15, a kąt ostry miarę α.

	√20−1
a) sinα=		,
	15

	1
b) cosα=
	4

	2
c) cosα=
	5

	1
No i podzieliłem sobie na dwa trójkąty i ze wzoru		*8*15*sinα, dlatego stąd było moje
	2

pytanie, czy te dwa trójkąty będą przystające, żeby to pole po prostu sobie pomnożyć przez 2 i otrzymać pole równoległoboku (2 razy pole trójkata)

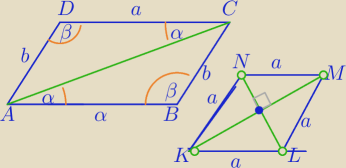
Mila: Salamandra przecież widzisz , że nawet na Twoim rysunku przekątna nie jest dwusieczną. 1) ΔABC≡ΔADC cech bkb Jeżeli równoległobok jest rombem to przekątne są prostopadłe, dzielą się na połowy i są dwusiecznymi kątów wewnętrznych.

salamandra: No i o to potwierdzenie mi chodziło, dzięki

salamandra: A jak udowodnić ze to dwusieczna? Jakoś z trójkątów równoramiennych? Mowa o rombie

Saizou : Tak, wystarczą trójkąt równoramienne

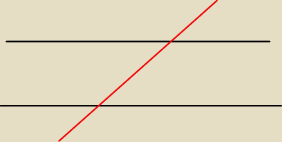
an: Szybka odpowiedź (po czasie) Patrzę i nie rozumiem, czy salamandra nigdy nie słyszała o prostych równoległych przeciętych trzecią prostą, bo przecież gdyby słyszała nie zadawałaby takich pytań

salamandra: Jaki to ma związek z dwusieczną?

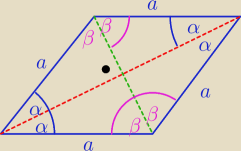
a@b: A no taki

salamandra: Już wiem, Saizou mi potwierdził to co teraz zrobiłaś

salamandra: Zdaję sobie sprawę, że czasami zadaje pytanie o to samo cyklicznie, jednak przy robieniu codziennie zadań z różnych działów, ciężko wszystko zapamiętać, szczególnie jak jakiegoś działu się nie lubi (w moim przypadku planimetrii/stereometrii). Po rysunku janka już mi się wszystko przypomniało.

a@b: Nie przejmuj się idź do przodu ... , dalej i dalej ... ( "trening czyni mistrza"

salamandra: taak, już i tak widzę postępy z planimetrii/stereometrii co nie zmienia faktu, że czasami te najprostsze zależności się zapomni