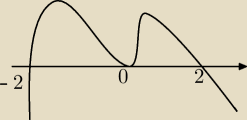
Ekstrema lokalne funkcji wulgarmaster: Pochodna funkcji f wyrażona jest wzorem f'(x)=4x²−x⁴. Wyznacz ekstrema lokalne funkcji. Wychodzi mi max dla −2 min dla 0 i max dla 2, ale w odpowiedziach są tylko 2 ekstrema, bez 0. Wytłumaczy ktos?

Szkolniak: brak zmiany znaku w x=0

salamandra: f'(x)= −x⁴+4x² f'(x)=0 ⇔ −x²(x²−4)=0 −x²(x²−4)=0 x=0 v x=2 v x=−2 max dla 2, min dla −2.

salamandra: Zauważ, że przy zerze ona nie zaczyna maleć, czyli do dwójki caly czas rośnie.

wulgarmaster: Dlaczego w 0 nie zmienia znaku? 0 wystepuje nieparzyście wiec wykres nie powinien przechodzić przez 0?

salamandra: 0 jest pierwiastkiem parzystokrotnym.

wulgarmaster: aaa no tak dobra dzięki teraz wszystko jasne

janek191:

	4		x5
f(x) =		x3 −
	3		5

f'(x) = x²*(4 − x²} = 0 ⇔ x = 0 lub x = − 2 lub x = 2 f ''(x) = 8 x − 4 x³ f ''(0) = 0 − punkt przegięcia w x = 0 f ''(−2) = − 16 + 32 = 16 > 0 − minimum lokalne w x = − 2 f ''(2) = 16 − 32 = − 16 < 0 − maksimum lokalne w x = 2