okrąg i styczna julik: znajdź współrzędne środków okręgów stycznych do prostych o równaniach x+2y+9=0 i2x−y−2=0 i przechodzących przez początek układu współrzędnych.

Mila:

	1		9
k: x+2y+9=0 ⇔y=−		x−
	2		2

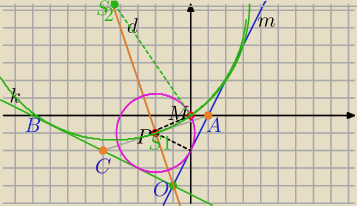
i m: 2x−y−2=0 ⇔y=2x−2 O=(−1,−4) m⊥k 1) środek okręgu stycznego do prostych k i m leży na dwusiecznej kąta AOB OA→=[2,4] OC→=|−4,2] |OA|=|OC| O=(−1,−4)→T_[−4,2]⇒C=(−5,−2) ΔAOC− Δrównoramienny Srodek AC: P=(−2,−1) prosta OP− dwusieczna : y=−3x+b −4=3+b, b=−7 d: y=−3x−7 równanie dwusiecznej S=(a,b)=(a,−3a−7) środek okręgu 2) równanie okręgu: (x−a)²+(y−b)²=r² |SM|=√a²+b²=r² Odległości d(S,k)=d(S,M)

|a+2b+9|
	=√a2+b2
√5

|a+2b+9|=√5a²+5b² |a+2(−3a−7)+9|=√5a²+5(−3a−7)² |−5a−5|=√50a²+210a+245 /² 25a²+50a+25=50a²+210a+245⇔

	22
a=−2 lub a=−
	5

	22		31
S1=(−2,−1) lub S2=(−		,
	5		5

	289
r12=5 lub r22=
	5

Pisz równania okręgów i sprawdzaj obliczenia

julik: dziękuję bardzo!