wykres marcus: proszę o pomoc nie rozwiązanie tylko wskazówki jak zrobić wykres dla jakich wartości parametru m równanie ma dokładnie dwa ujemne rozwiązania ||x−2|−|x+4|| zrobiłem założenia ze x≥2 ⋀x<2 i teraz ma to tylko odnieść do pierwszego modułu a do drugiego x≥−4⋀x<−4 tylko wtedy opuszczam pierwszy moduł dla x≥2 ? a co z drugim modułem opuszczać go dla x≥−4 a potem odwrotnie dla mniejszych ? zrobiłem tak i wyszły pary dwóch równoległych. Proszę o wskazówki co pierwsze zrobić, nie róbcie mi wykresu tylko co zrobić ?

salamandra: a gdzie jest m?

marcus: ||x−2|−|x+4||=m

salamandra: 1) x∊(−∞; −4) |−x+2−(−x−4)| = |6|=6 2) x∊<−4; 2) = |−x+2−x−4| = |−2x−2| g(x)= |−2x−2| x∊<−4; −1) → g(x)= −2x−2 x∊<−1; 2) → g(x)= 2x+2 3) x∊<2; ∞) |x−2−x−4| = |−6|= 6

Blee: 1) rysujesz |x−2| − |x+4| 2) dzielisz na trzy przedziały: a) x < −4 b) −4 ≤ < 2 c) x ≥ 2 3) nakładasz na wykres moduł 4) odczytujesz to czego szukasz

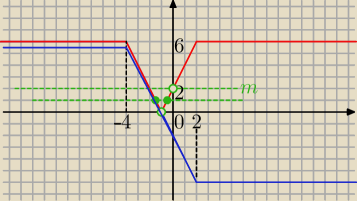
a@b: Niebieski wykres dla x∊(−∞, −4) f(x)=6 dla x∊<−4,2) f(x)= −2x−2 dla x∊<2,∞) f(x)= −6 czerwony wykres |f(x)| y= m dwa punkty po lewej stronie czerwonego wykresu tylko dla : m∊(0,2)

marcus: Dzięki salamandra tylko twoje tlumaczenie zrozumiałem. Blee to jakiś kosmos, narysowalem szpiczasty x−2 obok x+4 potem widzę przed tym x+4 znak minusa czyli zatsąpienie prawej częsci symetrycznym odbiciem w osi OY jego lewej na to wszytsko moduł, ale chocbym sie zesral to nie wychodzi stała y=6 to na moj mózg działa tylko takie piasnie jak salamandra i w tylku mnie strzela ze to tak dlugo trwa, a inni szybko to robia jak blee. a@b skad wiesz ze trzeba wziac od razu pod uwage tylko −2x−2 w tym przedziale x∊<−4,2> tam jeszcze wychodzi jak u salamandry 2x+2 ?

salamandra: Zauważ, że a@b wszystko dopiero na koniec „zamknęła” w ostatnia wartość bezwględna, stad ten drugi przedział 2x+2, to tak naprawdę −2x−2 ale obity względem osi OX