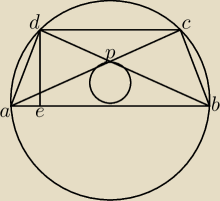
Trapez wpisany w okrąg - pole okręgu wpisanego w trójkąt mat: Trapez równoramienny ABCD o ramieniu długości 6 wpisany jest w okrąg, przy czym dłuższa podstawa AB trapezu, o długości 12, jest średnicą tego okręgu. Przekątne AC i BD trapezu przecinają się w punkcie P . Oblicz pole koła wpisanego w trójkąt ABP. |BD|=6√3, bo trójkąt ABD jest prostokątny. |DE|=3√3 z porównania pól. Trójkąt ABP jest podobny do trójkąta CPD, bo kąty wierzchołkowe, tak? Dlaczego

	2
|BP|=		|DB|?
	3

	12
Skala podobieństwa to k=		=2
	6

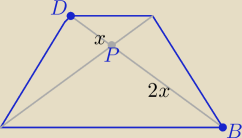a@b: |DB|=3x , |BP|=2x

	|BP|		2
to		= 2/3 ⇒ ......... |BP|=		|DB|
	|BD|		3

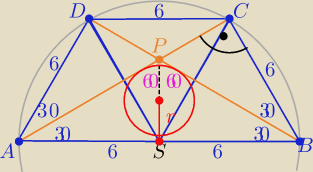a@b: Taki trapez składa się z trzech trójkątów równobocznych ( uzasadnij to zatem ΔABP jest równoramienny − rozwartokątny o kątach 30^o,30^o,120^o Z ΔASP o kątach 30^o,60^o, 90^o mamy: |AP|=|BP|= 4√3 , |AB|=12 i |PS|=2√3

	1
P(ABP)=		*|AB|*|PS| ⇒ P(ABP)= 12√3 obwód L(ABP)=12+8√3
	2

to ze wzoru P=rp mamy:

	12√3		6√3
r=		=
	6+4√3		3+2√3

P(koła) = πr² =.............. dokończ Odp: P(koła)= 36( 7−4√3) ===================

mat:

	2
Dziękuję, a jeszcze dlaczego |PS|=		h? A h to jest |DE|=3√3
	3

S to środek podstawy

mat: Wysłałem, zanim zobaczyłem drugą wiadomość

a@b: