Graniastosłupy Marcinkiewicz: a) Dany jest graniastosłup prawidłowy czworokątny, którego pole powierzchni bocznej jest 3 razy większe od sumy pól podstaw. Oblicz jego objętość, jeżeli pole koła opisanego na podstawie wynosi 18π. Pb = 3 * (2*a²) = 6a² 4ah = 6a²

	3
h =		a
	2

b) Dłuższa przekątna graniastosłupa prawidłowego szcześciokątnego tworzy z płaszczyzn podstawy kąt, którego cosinus wynosi 4/5. Pole podstawy wynosi 24√3. Oblicz długość krótszej przekątnej tego graniastosłupa. c) Dany jest graniastosłup prawidłowy trójkątny ABC A'B'C' o krawędzi podstawy dł. 6. Pole przekorju BCA' jest równe 18. Oblicz objętość graniastosłupa oraz cosinus kąta BA'C

Marcinkiewicz: A) P = πr² 18π = πr² r = 3√2 d = a√2 = 2 * r a√2 = 6 √2 a = 6 Pp = a² = 36

	3
V = Pp * H = 36 *		a = 36 * 9 = 324
	2

ite: a/ prawidłowo obliczone

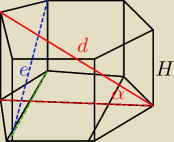
salamandra: b)

	4
cosα=
	5

a− bok jednego z sześciu trójkątów równobocznych w podstawie

2a		4
	=
d		5

10a=4d

	a2√3
P=6*
	4

	a2√3
24√3=6*		/ : 6
	4

	a2√3
4√3=		/ * 4
	4

16√3 = a²√3 48=3a² a=4 4d= 40 d= 10 sin²α+cos²α=1

	16
sin2α+		= 1
	25

	3
sinα=
	5

	H
sinα=
	10

H		3
	=
10		5

5H=30 H=6 odcinek zielony − dwie wysokości trójkąta równobocznego 2h=4√3 z tw. Pitagorasa (4√3)²+H²=e² 48+36=e² 84=e² e=√84=2√21 Nie daje gwarancji, że dobrze.

Marcinkiewicz: Wyszło mi tak samo, lecz zrobiłem troszeczkę inaczej.

salamandra: Nie masz odpowiedzi?

Marcinkiewicz: Niestety nie to zadania podane przez panią

salamandra: c) zrobiłeś?

Marcinkiewicz: ale po prostu są dwa sposoby w tym zadaniu, ja nie używałem jedynki trygonometrycznej, po prostu z cosinusa i wcześniejszym wyliczeniu ze wzoru a wyliczyłem dłuższą przekątną, później krawędź boczną i następnie trzeba tylko było znać zależność, że podstawa krótszej przekątnej to dwie wysokości trójkąta równobocznego, myslę, że nie masz tutaj żadnego błędu tak samo jak ja

Marcinkiewicz: właśnie się za to biorę

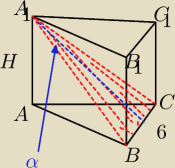
salamandra: P_ΔBCA₁ = 18

	6*h
18=
	2

36=6*h h=6 6²+3²=|A₁B|² |A₁B| = 3√5 H²+6²= (3√5)² H=3

	36√3
V=		*3
	4

V=9√3=27√3

	2√5
cosα= U{6}{3√5 =
	5

I tu mam dylemat jak zrobić cos2α, czy to będzie po prostu 2* cosα czy np.

	2√5		20		40		8
cos2α = 2cos2α − 1 = 2(		)2= 2(		) =		=
	5		25		25		5

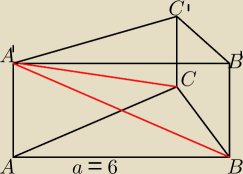
Marcinkiewicz: C) P_BCA'=18 V = ? cos BA'C = ?

Mila: salamandra b) dobrze, ale mając a i d mogłeś z tw. Pitagorasa obliczyć H.

Marcinkiewicz: hmm, dlaczego "H²+6²= (3√5)²"?

Marcinkiewicz: dobra, juz wiem, zle spojrzałem na obrazku

Marcinkiewicz: i jak zamieniłbyś cos 8/5 na stopnie?

Marcinkiewicz: chociaz w sumie, jakby ktos mogl to zweryfikowac to byloby spoko, ja nie jestem pewny tego cosinusa kąta, bo nie potrafie zbytnio tego zrobic

salamandra: Ja tez tego nie jestem pewien właśnie

salamandra: Widzę błąd− nie oddałem jedynki od 40/25

salamandra: Nie odjalem*

Mila: w c)

	36√3
V=		*3=27√3
	4

Z tw. Pitagorasa: b=|BA'|=|CA'|=3√5 Z tw cosinusów: a²=b²+b²−2*b*b*cosα a²=2b²*(1−cosα)

	6
cosα=
	10

	3
cosα=
	5

II sposób

	α		h		α		6		2
cos		=		⇔cos		=		=
	2		b		2		3√5		√5

	α		2
cosα=2*cos2		−1=2*(		)2−1
	2		√5

	8
cosα=		−1
	5

	3
cosα=
	5

=======

Mila: Narysować i pokazać wcześniejsze obliczenia?

Mila: salmandra : |cosx|≤1

salamandra: Nie odjalem od 8/5 jedynki− chochlik, czyli jednak mi wyszło

Marcinkiewicz: mozesz tylko narysować do C jakie zależności bierzesz pod uwagę, chciałbym po prostu to lepiej zobaczyć przy wyliczaniu cosinusa

salamandra: Ja czy Mila?

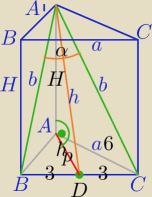
Mila: 1) Pole przekroju=18

1
	a*h=18
2

h=6 2)

	6√3
hp=		=3√3
	2

W ΔA'AD: h²=H²+h_p² 36=H²+(3√3)² H²=9, H=3 3)W BDA' : b²=3²+6² b²=45 (albo W ΔBAA' : H²+a²=b²⇔ b²=9+36=45 ) ======= dalej masz we wpisie : 17: 48

salamandra: zapomniałem o moim ulubionym tw. cosinusów i się niepotrzebnie bawiłem w podzielenie na dwa trójkąty

Mila: I dobrze, teraz masz nowe doświadczenie. Powtarzanie jest matką studiów.

a@b: Szczególnie "powtarzanie roku"