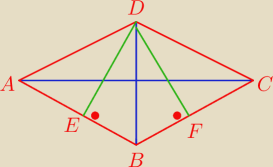
romb xyz: W rombie ABCD o przekątnych długości 4 i 8 poprowadzono z wierzchołka kąta rozwartego wysokości DE i DF Wykaż że pole trójkąta DEF stanowi 32% pola rombu

janek191:

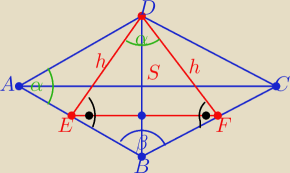
janek191: P = 0,5*8*4 = 16 I AB I = √4² +2² = 2√5 I DE I = h 2√5*h = 16

	8
h =
	√5

I ∡ BDE I = α

	h		8		2
cos α =		=		: 4 =
	DB		√5		√5

	1
sin α =
	√5

	4
sin 2α = 2*sin α*cos α =
	5

	64		4		128
PΔ = 0,5 h2*sin 2α = 0,5*		*		=
	5		5		25

więc

PΔ
	= 0,32 = 32%
P

a@b:

	1
P=		*4*8 =16 , a2=42+22 =20
	2

	4		64
P= a2*sinα ⇒ sinα=		i P2=a2*h2 ⇒ h2=
	5		5

	1		128
S=		h2*sinα ⇒ S=
	2		25

S/P=128/25*16 = 32/100 S=32%P ========