Geometria analityczna
Szkolniak: Dany jest trapez równoramienny o podstawach AB i CD. Oblicz współrzędne wierzchołka D wiedząc,
że A=(0,−2), B=(8,6), C=(3,7).
Moje postępowanie:
1) Wyznaczam równanie prostej AB w postaci ogólnej
2) Zapisuje równość pomiędzy długościami odcinków BC i AD
3) Zapisuje równość pomiędzy odległościami punktu D od prostej AB i punktu C od prostej AB
Jest inny sposób na rozwiązanie tego zadania?
Ponieważ moją metodą wychodzi bardzo wiele 'zbędnych' rozwiązań i muszę się sugerować domysłami
na podstawie rysunku na temat współrzędnych punktu D.
16 lut 02:05
Blee:
1) równanie prostej zawierającej odcinek AB
2) równanie prostej równoległej do (1) przechodzącej przez punkt C
3) wyznaczasz długość ramienia BC
4) wyznaczasz wzór okręgu o środku w A i promieniu |BC|
5) przecięcie się prostej (2) z okręgiem wyznaczasz dwa (jeżeli to prostokąt to jedno)
rozwiązania −−− punkt D
16 lut 02:18
Blee:
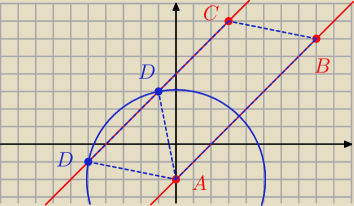
16 lut 02:22
Szkolniak: O właśnie, Twój punkt drugi i moim zdaniem łatwiej, bez okręgu:
1) Prosta równoległa do prostej AB przechodząca przez punkt C ma równanie y=x+4, zatem punkt
D=(x,x+4)
2) Równanie z jedną niewiadomą (x): |BC|2=|AD|2
Tak też by wyszło?
16 lut 02:24
Blee:
przecież to się sprowadza do tego samego
równanie okręgu (x−0)2 + (y + 2)2 = 26
|BC|2 = |AD|2 ⇔ 26 = (xD − 0)2 + (yD + 2)2
i podstawiasz yd = x+4 (zarówno w jednym jak i drugim przypadku
16 lut 02:28
Blee:
oczywiście ... można też policzyć w inny sposób (np wyznaczyć prostopadłe do tych prostych z
punktu A i B .. policzyć odległość punktu C od przecięcia prostopadłej przechodzącej przez B i
odłożyć tą odległość od przecięcia się prostej (2) i prostopadłej z punktu A) ... ale ten
sposób co napisałem wydaje się najszybszy i najmniej skomplikowany (najmniej miejsc do
popełnienia pomyłki)
16 lut 02:35
Szkolniak: Racja, bo ten sposób eliminuje mi po prostu zbędne (symetryczne) rozwiązania spowodowane
własnie tą odległością punktu od prostej, bo wychodzą mi równania dwóch prostych
Dzięki wielkie

16 lut 02:42

