Pole Bartek: Cześć mam pytanie jak wygladałby wzór na pole ograniczone krzywymi y=x y=2^x x=0 x=1 według osi oy według osi ox to ∫2^x−x ds od 0 do 1, ale jestem ciekaw jak zrobić to według osi oy

Jerzy: Co to znaczy wg osi ?

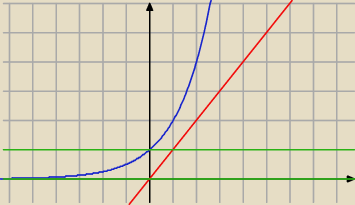
Blee: według osi OY albo: 1) wyznaczasz funkcje odwrotne i liczysz normalnie 2) robiąc rysunek patrzy i liczysz ∫_−∞⁰ 2^x dx + ∫₀¹ (1 − x) dx

Leszek: Tzn, pole powierzchni miedzy wykresem funkcji i osia OY zmieniamy funkcje na odwrotne na. y = 2^x ⇒ f⁻¹ = log₂x ⇒ y = log₂x

Jerzy: @Leszek, a której funkcji ?

Bartek: Czyli liczę funkcje odwrotne i dalej normalnie. I wychodzi mi ∫x−log₂x od 0 do 1 ale to mi nie pasuje. Pewnie coś źle zrozumiałem. Wiecie co robię źle?

Bartek: problem jest chyba z przedziałem na którym obliczam całkę

Blee: ale co Ci 'nie pasuje'

Bartek: Nie jestem pewien czy ∫x−log₂x od do 1 jest poprawna

Bartek: Chodzi mi o to że trzeba jeszcze chyba zmienić przedział na którym całkujemy

Bartek: Z wykresu wychodzi mi że to powinna być całka od 1 do 2 ale nwm skąd to się bierze

Blee: niby z jakiego wykresu Ci to wychodzi

Blee: dobra ... ja na początku przeczytałem że to jest y = 0 i y = 1