Napisz równanie okręgu o promieniu.. kykil24: Hej, mógłby ktoś to sprawdzić? Napisz równanie okręgu o promieniu √2 przechodzącego przez punkt A=(0,3) i stycznego do prostej o równaniu x−y+1=0. k: y=x+1 l: y=ax+b l ⊥k −> a=−1 3=0+b b=3 l: y=−x+3

⎧	(x−0)2 + (y−3)2=√2
⎩	y=−x+3

⎧	x2+x2=2
⎩	y=−x+3

⎧	x=1
⎩	y=2

o: (x−1)²+(y−2)²=√2²

Jerzy: Skąd masz równanie (x−0)² + (y−3)² = √2 ?

kykil24: √2²*

Jerzy: To pomijam.Przecież punkt A nie jest środkiem szukanego okręgu.

kykil24: Hmm faktycznie, to jak go wyznaczyć?

Jerzy: Co to jest prosta l i dlaczego przechodzi przez punkt A ?

Jerzy: Masz dwie niewiadome x_s i y_s więc musisz mieć dwa niezależne równania. Pierwsze, to równanie okręgu,drugie to odległość środka od stycznej.

Blee: 1) wyznaczasz proste (dwie) równoległe do prostej l, odległe od niej o √2 2) wyznaczasz równianie okręgu o środku A i promieniu √2 3) punkty przecięcia prostych (1) z okręgiem (2) wyznaczają ewentualne środki szukanych (bądź szukanego) okręgów

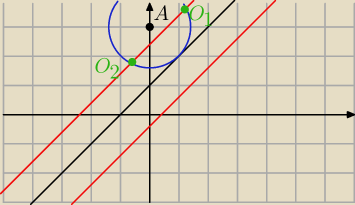
Blee: rysunek POGLĄDOWY −−− nie jest on w 100% dokładny

Jerzy: Blee, nie za bardzo kombinujesz. W moim sposobie dostaje układ dwóch prostych równań.

Blee: Bo okrąg (2) (na rysunku niebieski) NIE JEST styczny do prostej x−y+1=0 (czarna)

Blee: Jerzy ... z pewnością jest łatwiejszy sposób ... ja po prostu podchodzę do tematu w ten sposób aby skorzystać z jak najbardziej podstawowych wzorów (bo większości po prostu nie pamiętam ) I tutaj np. zrobiłem gafę, bo faktycznie niebieski okrąg będzie styczny do czarnej prostej: x−y+1 = 0 Natomiast źle narysowane są czerowne proste (co widać na pierwszy rzut oka

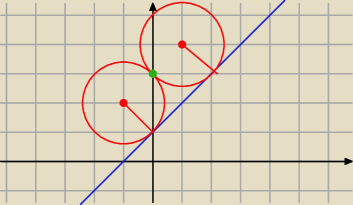
a@b: r=√2 S(a,b) k: x−y+1=0 A(0,3)∊o(S,r) to o: (0−a)²+(3−b)²=2 Odległość S od prostej k jest d=r=√2

|a−b+1|
	=√2
√2

|a−b+1|=2 ⇒ a−b+1=2 v a−b+1= −2 a= b+1 v a=b−3 o: (b+1)²+(b−3)²=2⇒ Δ<0 lub o: (b−3)²+(b−3)²=2 ⇒ b−3=1 v b−3= −1 ⇒ b=4 v b= 2 to a=1 v a= −1 są dwa takie okręgi o środkach S₁(1,4) , S₂(−1,2) i r²=2 teraz tylko .....podaj ich równania

Jerzy: I o to chodziło

kykil24:

|a−b+1|
	=√2
√2

to jest ze wzoru na odległość punktu od prostej?

Szkolniak: Tak