proszę o rozwiązanie
anna: Objętość ostrosłupa prawidłowego czworokątnego wynosi√6, a kąt między dwie−ma sąsiednimi
ścianami bocznymi ma miarę 120◦.
Oblicz pole podstawy tego ostrosłupa.
14 lut 22:05
a@b:
Pp=33√2
========
14 lut 23:39
anna: w tym zadaniu mam problem obliczenia wysokości ostrosłupa H
moje obliczenia to
3
√6 = a
2 *H
15 lut 08:07
a@b:
V=
√6 to a
2*H=3
√6
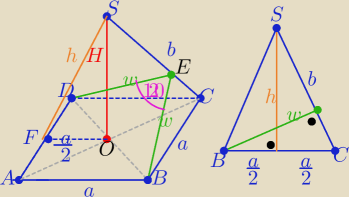
W ΔBDE: z tw. cosinusów
| | 1 | |
2a2=w2+w2+2w*w* |
| , bo cos120o= −cos60o=−1/2 |
| | 2 | |
| | a2 | | a2 | | a√2 | |
w ΔFOS : H2=h2− |
| w ΔOCS: (**) H2=b2− |
| , bo |OC|= |
| |
| | 4 | | 2 | | 2 | |
| | a2 | |
porównując H2 otrzymujemy (* ) b2−h2= |
| |
| | 2 | |
teraz w ΔBCS : P
Δ=a*h/2 i P=w*b/2 podstawiając za w=a
√6/3
| | 3 | |
i z (*) b2−h2=a2/2 ⇒ b2= |
| a2 |
| | 2 | |
| | a2 | |
to z (**) H2=b2= |
| ⇒ H2=a2 ⇒ H=a |
| | 2 | |
a
2*H=3
√6 ⇒ a
3=3
√6 ⇒ a=
3√3√6
to a
2=
3√9*6 −3
3√2
P
p=a
2=3
3√2
==============
15 lut 10:39
a@b:
Poprawiam zapis : a2=3√9*6=33√2
15 lut 10:42
15 lut 18:02
a@b:
Hej
Mila 
Gdzie się rąbnęłam? ( możesz wskazać
15 lut 18:03
a@b:
Ach ... już widzę
| | a2 | |
tu jest błąd ..... w (*) b2−h2= |
| |
| | 4 | |
| | 1 | |
zatem ... H= |
| a to a=√6 |
| | 2 | |
P
p=a
2=6
=======
15 lut 18:16
Mila:
Liczyłam trochę inaczej .
Dalej Inaczej.
Powinno być u Ciebie :
| | a2 | |
Porównując H2 ......b2−h2= |
| |
| | 4 | |
15 lut 18:29
a@b:
Tak znalazłam ten błędy zapis
( chochlik,który namieszał w obliczeniach
15 lut 19:11
anna: dziękuję bardzo
15 lut 19:14
a@b:
Popraw
Aniu ten mój błędzik
15 lut 19:16
anna: już poprawiłam i jeszcze raz dziękuję
15 lut 19:58
a@b:
15 lut 20:02