matura rozszerzona, dowód Julia: wykaż, że jeśli stosunek promienia okręgu wpisanego w trójkąt prostokątny do promienia okręgu opisanego na tym trójkącie jest równy √2 −1, to trójkąt ten jest równoramienny

Blee: r −−− promień wpisanego R − promień opisanego

	2P
r =
	a+b+c

	c
R =		(patrz trójkąt prostokątny wpisany w okrąg)
	2

r		a*b		√2		c
	= √2 − 1 −>		=		c −		−> (*)
R		a+b+c		2		2

z tw. Pitagorasa:

	(a+b)2 − c2		(a+b−c)(a+b+c)
a2 + b2 = c2 −> (a+b)2 − 2ab = c2 −> ab =		=
	2		2

	(a+b−c)(a+b+c)		√2		c
(*) −>		=		c −		−>
	2(a+b+c)		2		2

	a+b−c		√2		c
−>		=		c −		−> a+b = √2c
	2		2		2

wracamy do tw. Pitagorasa i podstawiamy za c:

	(a+b)2
a2 + b2 =
	2

2a² + 2b² − a² − 2ab − b² = 0 (a−b)² = 0 −> a = b c.n.w.

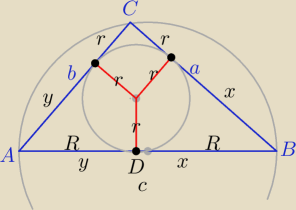
Mila: Z. ΔABC− Δprostokątny

r
	=√2−1
R

T. ΔABC− Δprostokątny równoramienny 1) r=R*(√2−1), c=2R W dowolnym Δ prostokątnym: a+b=2r+2R⇔a+b=2R√2 a+b=2R√2 /² a²+2ab+b²=2*(2R)² a²+b²=(2R)² z tw. Pitagorasa a²+2ab+b²=2*(a²+b²)⇔a²+b²=2ab a²−2ab+b²=0⇔ (a−b)²=0⇔a=b cnw

Eta: To jeszcze tak 2R=c , 2r=a+b−c

a+b−c		a		b		√2		√2
	=√2−1 ⇒		+		=√2 ⇒sinα+sinβ= √2=		+
c		c		c		2		2

α=β=45^o −−− trójkąt prostokątny równoramienny ♥♥♥♥♥♥♥♥♥♥♥♥♥

Bleee: Etus.... Trochę za bardzo na skróty poszłaś. Brak jasne objaśnienia skąd z

	√2
sina + sinb = √2 ma wynikać ze sina = sinb =
	2

a@b: No to dokończę α+β=90^o

	α−β
sinα+sinβ= √2cos
	2

	α−β
cos		=1
	2

α−β=0 α=β =45^o

a@b: @Blee .... teraz pasuje ?

Julia: Bardzo wszystkim dziękuję, miłego dnia