stereometria
salamandra: Skoro wysokość ostrosłupa prawidłowego trójkątnego pada na środek jego podstawy (na punkt
przecięcia dwusiecznych?), to jak to jest, że w zadaniu:
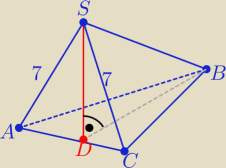
Podstawą ostrosłupa ABCS jest trójkąt równoboczny ABC o boku dlugosci 8. Punkt D jest środkiem
krawędzi AC, a odcinek DS jest wysokością ostrosłupa. Krawędzie AS i CS mają długość 7.
To jak to jest, że w tym zadaniu wysokość jest jednocześnie wysokością ściany bocznej i wcale
nie jest po środku?
13 lut 23:32
Mila:
To nie może to być ostrosłup prawidłowy trójkątny. Coś z treścią pomyliłeś.
13 lut 23:38
a@b:
13 lut 23:39
13 lut 23:41
a@b:
Ale nie jest prawidłowy !
Wysokość jest w ścianie bocznej
13 lut 23:42
salamandra: "Prawidłowość" nie określa trójkąt równoboczny w podstawie?
13 lut 23:45
Mila:
Jak tam zdrowie? Poprawiło się?
13 lut 23:45
a@b:
Szukany kąt to: |∡SBD|
13 lut 23:46
salamandra: Ja zadanie mam rozwiązane, tylko zachciało mi się pofilozofować

13 lut 23:47
a@b:


13 lut 23:47
salamandra: Czyli mimo, że trójkąt równoboczny jest w podstawie, to nie jest to ostrosłup prawidłowy? Teraz
to mnie zaskoczyłaś.
13 lut 23:49
Mila:
Przeczytaj definicję ostrosłupa prawidłowego

13 lut 23:53
13 lut 23:56
salamandra: Byłem pewien, że to podstawa o tym decyduje, kto wie, czy ta niewiedza nie kosztowałaby za dużo

13 lut 23:56
a@b:

dobre na pamięć !

13 lut 23:58
salamandra: Zapamiętam

dobranoc
14 lut 00:00
a@b:

14 lut 00:00






 dobre na pamięć !
dobre na pamięć ! 
 dobranoc
dobranoc
