Geometria analityczna
Patryk: Cześć,
Mam takie zadanie z geometrii analitycznej ale wychodzi mi delta, której nie da się
spierwiastkować a powinna.
Prosta x−y−5 = 0 zawiera bok AB trójkąta ABC, prosta 2x+y−13 = 0 zawiera bok BC a prosta 3x−y−7
= 0 zawiera dwusieczna kąta BAC. Znajdź wierzcholki trójkąta.
Wierzchołki A i B znalazłem z przecięcia się prostych: A=(1,−4), B=(6,1) natomiast C=(x,
−2x+13) chciałem z twierdzenia o dwusiecznej i stosunku odcinków trójkąta na jakie dzieli.
|AB| = 5
√2
|BD| = 2
√5 // D − punkt przecięcia dwusiecznej i prostej BC
|CD| =
√(x−4)2+(8−2x)2
|AC| =
√(x−1)2 + (17−2x)2
po obliczeniach wychodzi mi równanie −3x
2 + 20x + 36 = 0
13 lut 21:40
: √Δ ≈ 29
13 lut 21:44
Patryk: Nie powinno tak wyjść, gdzieś mam błąd...
13 lut 21:55
Mila:
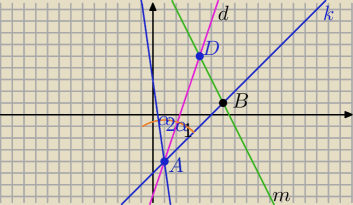
k: x−y−5 = 0 ⇔y=x−5, tgα=1
m: 2x+y−13 = 0 ⇔y=−2x+13
d: 3x−y−7=0 ⇔y=3x−7 dwusieczna kąta BAC, tgβ=3
1) Punkty przecięcia prostych:
A=(1,−4) , B=(6,1)
2) tgα
1 − tangens kąta między prostymi d i k
| | |tgα−tgβ| | |
tgα1= |
| , α1− kąt ostry |
| | 1+tgα*tgβ | |
| | 3−1| | | 2 | | 1 | |
tgα1= |
| =| |
| |= |
| |
| | 1+3*1 | | 4 | | 2 | |
Równanie prostej AC:
y=ax+b,
| | 1 | |
tgα2= |
| − tangens kąta między prostymi d i AC |
| | 2 | |
1+3a=2(a−3)
a=−7
lub
1+3a=2*(3−a)
a=1 nie odpowiada war. zadania
y=−7x+b i −4=−7+b, b=3
AC: y=−7x+3
C− Punkt przecięcia :
y=−7x+3
y=−2x+13
C=(−2,17)
Taką masz odpowiedź ?
13 lut 23:16
a@b:
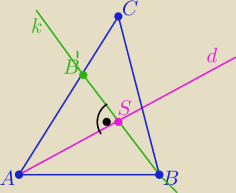
A(1,−4) , B(6,1)
d⊥ k i S jest środkiem odcinka BB
'
Napisz równanie prostej k⊥ d i przechodzącej przez B
rozwiąż układ równań prostych k i d otrzymasz S
Wyznacz współrzędne punktu B
'
Prosta AC ma równanie takie jak prosta AB
'
wyznacz to równanie
Rozwiązując układ równań prostej AC i BC o trzymasz
C( −2,17)
=========
13 lut 23:21
Mila:
Tak jest lepiej, zapomniałam o symetrii. Czas spać
13 lut 23:51
a@b:
No to
Patryk ma dwa sposoby
13 lut 23:57
: i już daaaawno poszedł spać
14 lut 10:27
Patryk: Tak, właśnie wstałem, musiałem się wyspać
Odpowiedź to C=(−2,17), dzięki za podrzucenie
metody.
PS: siedzę przy matmie do 1.00 w nocy więc do maturki będzie ciekawie
14 lut 20:14
Patryk: Jeszcze jedno pytanie, czyli |BS| = |B'S|?
14 lut 20:42
Mila:
Tak.
B' jest puntem symetrycznym do B względem dwusiecznej.
14 lut 21:14
Patryk: Ok, a z czego to wynika, że te odcinki są równe? Bo sam na początku bym na to nie wpadł.
14 lut 22:33
: tylko pamiętaj, że matura zaczyna się o 9 rano
14 lut 22:44
Mila:
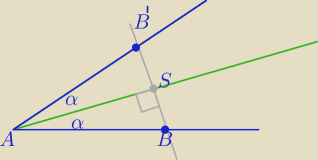
ΔASB≡ΔASB'
14 lut 22:45
Patryk: Dziękuje za rozrysowanie
15 lut 00:02
a@b:
15 lut 00:11