relacja równoważności logika: Rozważamy relację równoważności na R zdefiniowaną przez: x ~ y ⇔ sinx = siny (1) Wyznacz [0]_~ (2) Wyznacz [1]_~ (3) Wyznacz zbiór ilorazowy tej relacji (1) [0]_~ = {y ∊ R: yR0} = {y ∊ R: siny = sin0} = {y ∊ R: siny = 0} = {2kπ: k ∊ Z} (2) [1]_~ = {y ∊ R: yR1} = {y ∊ R: siny = sin1} = {1 + 2kπ: k ∊ Z} ∪ {π − 1 + 2kπ: k ∊ Z} (3) R/_~ = {[x]_~: x ∊ R} = {R} (?) Chociaż ostatniego nie jestem pewien. Na pewno to jest zbiór zbiorów, tylko, czy dobrze go określam?

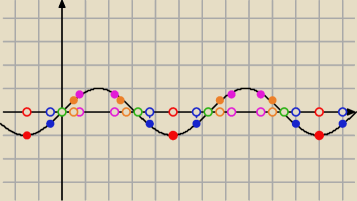
ite: (3) to zbiór zbiorów wyznaczonych przez liczby z przedziału <0, 2π), rysunek wyszedł zabawny ale może chyba oddaje ideę

logika: Tak coś też myślałem, a raczej sobie uświadomiłem. Suma tych zbiorów jest równa R. Czy takie uzasadnienie w postaci rysunku jest wystarczające?

Pytający: Rysunek jest zbędny, to tylko dodatek (acz bardzo urokliwy, Ite! ). W zasadzie: (3) R_/~ = {[x]_~: x ∊ ℛ} jest poprawną odpowiedzią, przecież właśnie to oznacza ten zapis. A jeśli chcesz "upraszczać", to możesz np. tak jak napisała Ite: R_/~ = {[x]_~: x ∊ <0, 2π)}, albo jeszcze bardziej:

	−π		π
R/~ = {[x]~: x ∊ <		,		)}.
	2		2

Ważne, żebyś zawarł w swym zapisie każdą klasę abstrakcji.

Pytający: Aha, i jeśli masz coś oznaczone jako R i w tym samym kontekście odnosisz się do zbioru liczb rzeczywistych, to dobrze użyć innego oznaczenia (ℛ). Przeważnie da się domyślić, o co komu chodzi, ale lepiej nie pozostawiać wątpliwości.

ite:

	−π		π
A ten mniejszy przedział może być <		,		> ? Żeby 1 do niego należało?
	2		2

Pytający: Ba, nawet musi! (a właściwiej ten mój nie może, a Twój jest w porządku) Mój błąd, rozpędziłem się z tym zawężaniem. Cytując siebie: "Ważne, żebyś zawarł w swym zapisie każdą klasę abstrakcji.", nie to co ja wyżej.

Pytający: Logika, i jeszcze masz błąd na końcu w (1), powinno być: ... = {kπ: k ∊ ℤ}

logika: Faktycznie, faktycznie. I w zasadzie tak, niby sam zapis jak w (3) jest już sam w sobie odpowiedzią, ale jeszcze trafię na kogoś, komu tego nie przetłumaczę i punkty polecą Dziękuję za wyjaśnienia