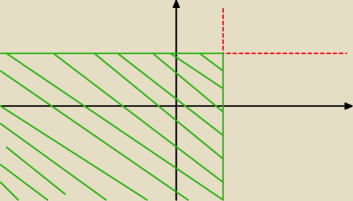
relacje logika: Zdefiniujmy częściowy porządek <R², ≤> poprzez <x, y> R <x', y'> ⇔ x ≤ x' ∧ y ≤ y' (1) Narysuj w układzie współrzędnych zbiór punktów porównywalnych z <1, 2> (2) Wyznacz kres górny zbioru {<x, y>: x² + y² = 1} = A. (3) Naszkicuj zbiór D, który ma jeden element maksymalny, ale nie ma elementu największego. (1) Czyli tak, bierzemy takie elementy <x, y>, że są w relacji z <1, 2>. Więc otrzymujemy: x ≤ 1 ∧ y ≤ 2. Wobec tego to będzie ten cały zielony obszar? Pionowe proste to x = 1 oraz y = 2. (2) Kres górny to najmniejsze ograniczenie górne, czyli w tym wypadku taki element <a, b> ∊ R², że: ∀_{<x, y> ∊ A} <x, y> ≤ <a, b> Wobec tego wszystkie te elementy muszą być porównywalne z tym jednym. Czy w takim razie będzie to punkt przecięcia prostych x = 1 oraz y = 1, to jest punkt <1, 1>? (3) Skoro zbiór ma mieć jeden element maksymalny, ale ma nie mieć największego, to nie może być ograniczony. No i tu nie bardzo wiem, jak się za to zabrać. Jakieś wskazówki?

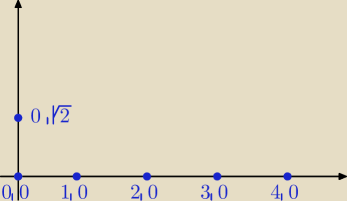
ite: /na rysunku są zaznaczone uporządkowane pary liczb/ (3) proponuję tak zbiór D to zbiór par: D={<0,√2>, <0,0>, <1,0>, <2,0>, <3,0>,<4,0>,...} <0,0>R<0,√2> <0,0>R<1,0> <1,0>R<2,0> para jest <0,√2> jedynym elementem maksymalnym, największy nie istnieje.

logika: O, bardzo fajnie Dziękuję

ite: Ja określenie: element <x, y> jest porównywalny z <1, 2> rozumiem jako <1, 2>R<x, y> czyli 1≤x ∧ 2≤y ? ?

logika: Hm, no właśnie, to też dobre pytanie. Czy jeśli <x, y> jest porównywalny z <1, 2>, to należy pisać <1, 2>R<x,y> czy może <x,y>R<1,2>? O ile w relacji równoważności nie ma to znaczenia, o tyle w liniowym porządku już tak.

logika: Oczywiście miałem na myśli częściowy porządek, choć liniowy również się nada.

ite: Ja to tak rozumiem: <x, y> zbiór punktów porównywalnych z <1, 2> → tworzą te dla których <1, 2>R<x, y> <x, y> zbiór punktów z którymi jest porównywalna para <1, 2> → tworzą te dla których <x,y>R<1,2> Ale często jestem jedyna, która akurat tak rozumie znaczenie jakichś zwrotów : )

logika: Okej, może ktoś jeszcze się wypowie, bo faktycznie nie wiem już które z którym się porównuje

Kacper: Dla mnie zbiór punktów porównywalnych to "większe" i "mniejsze" czyli <x,y>R<1,2> oraz <1,2>R<x,y> Ale ja miałem to tak dawno temu

Kacper: Znalazłem coś takiego w necie: Mówimy, że elementy x,y są porównywalne w tym częściowym porządku, gdy xRy lub yRx

logika: No właśnie też znalazłem informację, że to będzie suma tych dwóch zbiorów

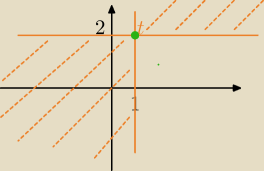
ite: to wtedy tak

logika: Dziękuję

ite: Kacper ja też, bo sobie coś rozjaśniłam : )