całki pytanie:

	1
Czy pole obszaru ograniczonego h(x)=		,y1=1,y2=16 trzeba liczyć osobno od −1 do 0 suma
	x4

od 0do 1 i podwoić czy można od razu od −1 do 1. Które funkcje będą tu miały znaczenie?

Blee: skoro liczysz ∫₋₁⁰ coś tam dx + ∫₀¹ (coś tam) dx to po co 'podwajać' później Zrób rysunek to będziesz wiedział które funkcje mają znaczenie Trzecia rzecz ... czemu mówisz o całkowaniu w granicach <−1 ; 1>

Blee:

	1
jak dla mnie to całkujesz w granicach		, 1
	2

pytanie: Ok czyli granicą górna to y=16 a dolną to h(x) i całka −1do0 + całka z takich samych funkcji od 0do1?

pytanie: Aha bo −1 jest ograniczeniem dolnym i ten punkt nie należy do wykresu funkcji a czemu wtedy 1 należy?

Blee: dlaczego chcesz całkować 'do' / 'od' 0 ? Wyjaśnij mi to

Blee: zrobiłeś szkic wykresu

pytanie: Nie powinny być dwie (z tymi samymi funkcjami) ∫<−1,−1/2>+∫<1/2,1>

pytanie: Tak

pytanie: 0 nie nalezy źle powiedziałem

Blee:

	1
2*(∫01/2 (16 − 1) dx + ∫1/2 1 (16 −		) dx) = ...
	x4

Blee:

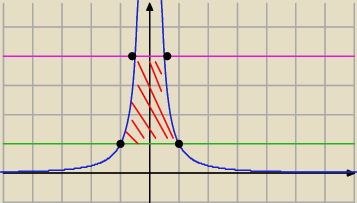
	1
analogiczny obszar (tylko tutaj h(x) =		a y2 = 4
	x2

pole tego typu obszaru masz policzyć

pytanie: Pytałem się bo na moim rysunku słabo to widać

pytanie: Bo ciężko na kartce się to rysuje

pytanie: Dziękuję ci bardzo