Planimetria salamandra: W romb ABCD wpisano okrąg. Długość boku rombu: 10, wysokość: 8. Obrano na ramieniu AD punkt F, taki ze F dzieli bok na dwa. E jest punktem styczności okręgu do ramienia AD. Oblicz odległość FE. Zadanie z dzisiejszego sprawdzianu, na telefonie ciężko zrobić rysunek. Wyszło mi 3, bo promień okręgu to 4. Wysokość opuszczona z ramienia BC to 8, wiec ten odcineczek od B do kata prostego z wysokości wynosi 6, wiec podstawa AB z tym wynosi 16, z Pitagorasa wyznaczyłem przekątna. Połowa przekątnej to będzie odległość od O do A, z Pitagorasa wyznaczyłem AE. Różnica miedzy AF a AE to = 3, i to szukany odcinek?

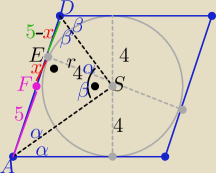
a@b: h=8=2r ⇒ r=4 z podobieństwa trójkątów ASE i DSE z cechy (kkk) r²=|AE|*|ED| 16=(5+x)*(5−x) ⇒ x²=9 i x∊(0,5) x=|FE|=3 =========

Leszek: Czy punkt F to srodek boku AD , jezeli tak to FO = 5 , EO = 4 i z trojkata prostokatnego EFO , EF = 3 , 0 srodek okregu

salamandra: No to mam dobrze

salamandra: Jak zwykle troche pod prąd, ale wyszlo

a@b:

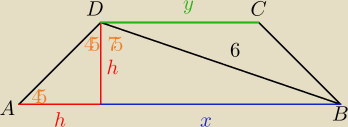
salamandra: A zadanie: w trapezie równoramiennym ABCD kat ostry ma 45 stopni. Przekątna ma 6 i tworzy z ramieniem kat 120 stopni. Wyznacz długości podstaw.

a@b: a= 3√6 , b=3√2 ==============

salamandra: Tez dobrze uf dziękuję

Saizou :

	h
cos75=
	6

	√6−√2
cos(75)=cos(30+45)=...=
	4

z Pitagorasa masz x y=x−h

salamandra: Ja zrobiłem z tw. Sinusów. Później napiszę swoje rozwiazanie

a@b: Też dobrze

salamandra:

AB		6
	=
sin120		sin45

√2		√3
	* AB = 6*
2		2

√2
	* AB = 3√3 / * 2
2

√2AB = 6√3 / * √2 2AB= 6√6 AB=3√6

DC		6
	=
sin30		sin135

	√2
3=DC*		/ * 2
	2

6=DC*√2 / * √2 6√2 = 2DC DC=3√2

salamandra: Do tego zadania z rombem, był jeszcze podpunkt, którego nie ruszyłem, ale ciekaw jestem rozwiązania. FGHJ są środkami boków rombu. Oblicz promień koła opisanego na tym czworokącie. Strzeliłem tylko, że R=5, ale to czysty strzał.

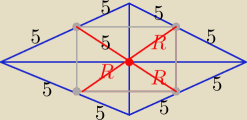
a@b: No i dobrze "strzeliłeś'

salamandra: A skąd to wynika? Nie widzę tego

Mila: No to całkiem nieźle napisałeś ten sprawdzian, ale mogłeś lepiej, bo tłumaczyłyśmy podobne problemy i dużo pracowałeś.

salamandra: Większości zadań nie pamiętam, a arkusza nie mam, zapamiętałem te, z którymi miałem wątpliwości. Mam źle tylko to wyżej, no bo nie uzasadniłem, tylko strzeliłem.

Mila: Odcinek łączący środki dwóch boków trójkąta ..... nie było tłumaczone?

salamandra: Coś było, ale nie pamietam