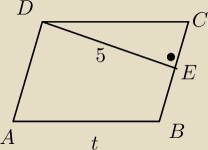
planimetria salamandra: 1. na rysunku czworokąt ABCD jest rombem. Zatem kąt rozwarty tego rombu ma miare? t= 5√2 DC=t EC²+5²=(5√2)² EC²+25=50 EC=5 więc DCE=45 stopni, to kąt rozwarty = 135 stopni?

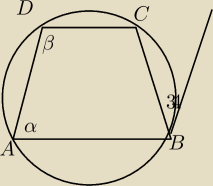
salamandra: 2. w trapezie ABCD wpisanym w okrąg o środku O, boki AD, DC, BC mają taka sama długość. Zatem α i β=? tam, ten kąt to 34, słabo widac na rysunku, nie wiem szczerze co mogę z tego kąta wywnioskować?

Blee: 1) Wyliczanie EC jest zbyteczne

	5		√2
sin(∡ECD) =		=		−> ∡ECD = 45o
	5√2		2

więc rozwarty = 180 − 45 = 135

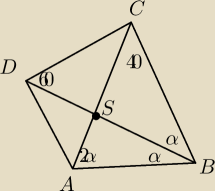
salamandra: Na czworokącie ABCD przedstawionym na rysunku mozna opisać okrąg. Zatem miara kąta DAB jest równa? ABC jest trójkątem równoramiennym, więc 180−40 = 4α α=35 2α=70 Więc kąt SDA musi być równy 50, aby zachodził warunek opisywalności. W trójkącie CSB, kąt CSB musi być 105, jako uzupełnienie do 180 Kąt DSA wierzchołkowy= 105, więc kąt DAS =25, więc DAB = 2α+25 = 95. Dobrze?

Bleee: 2) rozumiem że przy tym kącie 34^o masz styczną do okręgu. W takim razie α = 90 − 34 β = 180 − α

salamandra: No właśnie Blee nie mam pewności, że to styczna, wcale mi to na styczną nie wygląda

salamandra: odpowiedzi sa: α=34 i β=146 α=42 i β= 138 α=52 i β=128 α=68 i β=112

salamandra: https://imgur.com/a/DAdTLny

Bleee: 3) trochę krocej: Masz α W takim razie z trójkąta BCD część kąta przy C = 45 Warunek wpisania czworokąta: szukany kat = 180 − 40 − 45 = 95

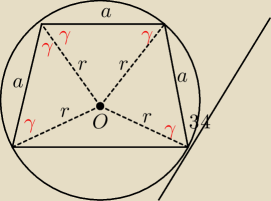
Blee: 2) masz trzy przystające trójkąty równoramienne. γ + 34 = 90 −> γ = 56 β = 2γ = 112 α = 180 − β = 68

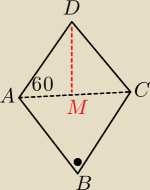
salamandra: ABCD jest deltoidem. Dłuższa przekątna tego deltoidu ma dlugosc? |AB|= 4√2 Więc CB również 4√2, ABC jest "połową kwadratu", więc AC= 4√2{2} = 8.

	DM		DM
Dzielę ΔADC na dwa, tg60=		=
	AM		4

	DM
√3 =
	4

4√3 = DM

	1
BM nie będzie po prostu połową przekątnej "kwadratu"?, więc		*AC = 4
	2

więc DB= 4√3+4?

salamandra: A skąd Blee wynika, że γ+34 = 90? Czyli to jednak styczna?

Blee: no oczywiście że jest to styczna ... tyle że styczna tworzy kąt 90^o z promieniem a nie bokiem trapezu (co początkowo przyjąłem)

salamandra: Rozumiem, jednak z rysunku w zadaniu wcale nie wynika, ze to styczna Jak mi potwierdzisz jeszcze ten deltoid będę mega wdzięczny

Blee: Dobrze. 4) Trochę inne podejście: |AB| = 4√2 ∡BAC = 45^o (bo ΔABC jest równoramienny)

	|AB|
|AC| =		= 4*2 = 8
	cos 45o

	a√3
ΔACD jest równoboczny .. h =		= 4√3
	2

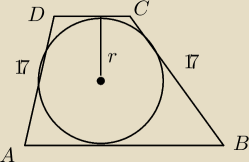
salamandra: Dzięki.... Jeszcze jedno ale to już opcjonalnie, Na okregu o srodku O i promieniu 7,5 opisano trapez. Ramiona mają dlugosc 17. Więc podstawy maja dlugosc? 2r= h h= 15

	a−b
Rozumiem ze musze poprowadzic z wierzcholkow C i D wysokosci i jakoś się bawić		?
	2

salamandra: Czy linią środkową, która będzie promieniem? (dwoma promieniami), bo chyba w połowie ramion jest styczność okręgu z ramionami prawda?

Blee: 10:34 −−− nie. To ma miejsce jedynie jeżeli trapez jest kwadratem Ale wiesz, że h = 15

a−b
	= √172 − 152 = 8
2

(a−b) + 2b = 34 −> b = 9 −> a = 25

salamandra: A skąd ta ostatnia linijka wynika? To 34?

salamandra: Ok , z warunku wpisywalnosci okręgu w czworokąt

salamandra: Dzięki Blee raz jeszcze, większość z tych zadań dostałem na teście, co prawda z innymi danymi, ale gdybyś nie potwierdził, że dobrze robię, to pewnie bym kombinował