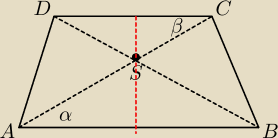
planimetria salamandra: Przekątne trapezu równoramiennego ABCD przecinają się w punkcie S . Przekątna AC tworzy z

	3
dłuższą podstawą AB kąt α i z ramieniem AD kąt β takie, że sin α =		i sinβ =
	5

	5
		.
	13

Pole trapezu ABCD jest równe 448. Oblicz pole trójkąta ABD . Czy mogę dorobić sobie te czerwone wysokości, aby móc jakkolwiek skorzystać z podanych wartości sinusa? Czy jest na to jakiś inny sposób?

:.: : Popraw rysunek, chodzi o kąt β.

salamandra: No właśnie zauważyłem, w tym momencie już nie mam pomysłu, bo tam ładnie bym miał z wysokością i podziałem podstaw na dwie równe części.

:.: :

	3
sinα=
	5

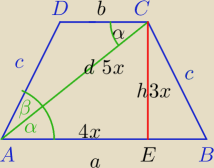
d=5x, h=3x, ⇒|AE|=4x x− wspólna miara

	a+b
|AE|=
	2

a+b
	*h=448
2

1) oblicz d,|AE|,h 2) W ΔACD z tw sinusów :

d		b
	=		oblicz b
sin(180−(α+β))		sinβ

Mila: I jak, rozwiązałeś?

salamandra: Poleciałem z następnymi i o nim zapomniałem, wrócę do niego zaraz

Mila: Jak postępuje praca?

salamandra: 4x*h=448 h=3x 4x*3x=448 12x²=448

	4√21
x=
	3

	16√21
|AE|=4x=
	3

	12√21
h= 3x=		= 4√21
	3

Dobrze do tego momentu?

salamandra:

	4√21		20√21
d=5*		=
	3		3

	25		144		12
cosβ = √1−		= √		=
	169		169		13

	9		16		4
cosα = √1−		=√		=
	25		25		5

d		b
	=
sin(α+β)		sinβ

d		b
	=
sinα*cosβ+cosα*cosβ		5   13

d		b
	=
35*1213+45*1213		5   13

20√213		b
	=
8465		5   13

	125√21
b=
	63

a+b
	= 4x
2

a+125√2163		16√21
	=
2		3

	125√21		8√21
a+		=
	63		3

Poddaję się w tym miejscu, już wiem, że jest źle

Mila: Masz odpowiedź do zadania? Zacznę liczyć, napisz.

a@b: P=323

Mila: Wpisuj Eta, jeśli korzonki już wyzdrowiały

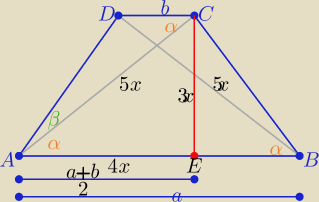
a@b: P(trapezu)= 12x² ⇒ x²=112/3

	1		3
P(ABD)=		*5x*a*sinα ⇒P(ABD)=		ax
	2		2

Z tw. sinusów w ΔADC:

	5x*sinβ		56
b=		, sin(α+β)=............=
	sin(α+β)		5*13

	125x
b=
	56

	323
a+b=8x ⇒ a= 8x−b ⇒ a=		x
	56

	3		323		112
P(ABD)=		*		x2 i x2=
	2		56		3

P(ABD)=323 ==========

salamandra: Widzę ,że przy sin(α+β) gdzieś mam błąd w takim razie, ale wydaje mi się, że wszystko dobrze wyliczyłem.

Mila: Masz pomyłkę. Dorysuj drugą przekątną i zaznacz kąty . Dokończyłam Twoje rachunki.

	56
sin(α+b)=
	65

	25
b=		d
	56

	1		1		1		25
PΔDCB=		b*d*sinα=		*		*		*d2*sinα
	2		2		2		56

	25		25√21		3
=		* (		)2*		=125
	56		3		5

P_ABD=448−125=323 Zostaw dzisiaj to zadanie, jutro popatrzysz.

salamandra: Zależy, czy po sprawdzianie będę w nastroju, żeby jeszcze planimetrię tykać mimo to dziękuję i do jutra

Mila: Co to za pesymizm? Powodzenia

Patryk: Rozumiem kolegę... też nie lubię planimetrii szczególnie zadań z samymi literkami i kątami

salamandra: Pesymizm tylko i wyłącznie dlatego, że wszystkie zadania, które dzisiaj zrobiłem z książki/ze zbioru/z internetu, wyrywkowo z zeszytu, które robiłem z miesiąc temu rozwiązałem niemalże bezbłędnie, a na sprawdzianie będą kosmiczne zadania, taki już urok wydawnictwa mojej książki i ich sprawdzianów.

Saizou : salamandra uczysz się dla siebie i swojej własnej wiedzy, sprawdzian to nie wszystko

salamandra: Taa, oceny mało mnie interesują, jednak zawsze gdy wydaje mi się, że umiem, to na sprawdzianie się okazuje, że dane zadanie widzę pierwszy raz na oczy mimo korzystania z wielu źródeł

Saizou : Stres też robi swoje, wiec na ludzie podejdź