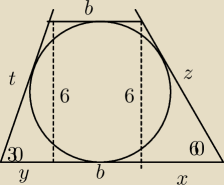
planimetria salamandra: W trapezie opisanym na okregu katy przy dłuzszej podstawie maja miary 30 i 60, a długosc wysokosci tego trapezu jest równa 6. Sporzadz odpowiedni rysunek i oznacz jego elementy. Oblicz pole trapezu oraz długosci jego podstaw.

	6
tg60=
	x

	6
√3=
	x

x=2√3

	6
tg30=
	y

√3		6
	=
3		y

y=6√3

	6
sin30=
	t

1		6
	=
2		t

t=12

	6
sin60=
	z

√3		6
	=
2		z

z=4√3 Z warunku wpisywalności okręgu w czworokąt: t+z=2b+x+y 12+4√3=2b+8√3 2b=12−4√3 b=6−2√3 a=6−2√3+2√3+6√3 = 6+6√3

	(6+6√3+6−2√3)*3
P=		= (12+4√3)*3=36+12√3 = 12(3+√3)
	2

jest ok?

Blee: x i y nie musisz wyliczać wystarczy wyliczyć t i z (w końcu a+b = (x+y+b) + b = t+z)

	t+z
I wtedy P =		*6 = ....
	2

Blee: trochę szybciej (bez zbytecznych obliczeń) ... wynik wyjdzie oczywiście ten sam

salamandra: No tak, ciekawe spostrzeżenie, które chyba będzie mi potrzebne przy nastepnym zadaniu: Dany jest trapez opisany na okręgu, którego kąty przy jednej podstawie są ostre, oraz którego pole jest równe 168. Przekątne dzielą ten trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów jeżeli ramiona trapezu mają długości 13 i 15.

	28*h
Więc jeśli założę, że 13+15=a+b, to P=		i z tego wyliczę wysokość itd?
	2

Blee: Tak ... ale niestety i tak będziesz musiał wyznaczyć a i b w tym zadaniu, aby móc obliczyć

	b		hb
proporcję		=		co będzie potrzebne do policzenia pól dwóch podobnych
	a		ha

trójkątów (o podstawach odpowiednio b i a) Dwa pozostałe trójkąty (których podstawami są ramiona trapezu) będą miały to samo pole

Blee:

P1		b*hb		hb		b
	=		gdzie hb + ha = h oraz		=
P2		a*ha		ha		a

P₃ = P₄ (ponieważ P₂ + P₃ = P₂ + P₄ <−−− ta sama podstawa (a) i wysokość (h) )

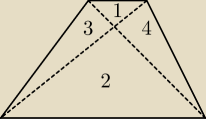
Blee: Natomiast trójkąty (1) i (2) są podobne −−− cecha KKK

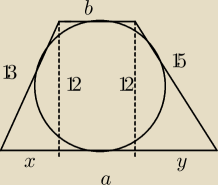
salamandra: 13+15 = a+b P=168

28*h
	=168
2

14h=168 h=12 x²+12²=13² x=5 12²+y²=15² y=9 13+15=2b+x+y 28=2b+14 2b=14 b=7

⎧	b=7
⎩	a=21

a
	=3
b

więc wysokość trójkąta nr 2= 9 wysokość trójkąta nr 1 = 3 Nie wiem skąd wynika, że pole 3 i 4 będzie identyczne?

Blee: Napisałem Ci w nawiasie zauważ, że

	a*h
P2 + P3 =
	2

także

	a*h
P2 + P4 =
	2

więc P₂ + P₃ = P₂ + P₄ ⇒ P₃ = P₄

salamandra: Aha, aż w tę stronę Co będzie podstawą trójkąta 3 lub 4? i jego wysokością?

Blee: Podstawami będą ramiona ... ale to nie jest ważne P₃ + P₄ = P_trapezu − P₁ − P₂ A P₁ i P₂ już znasz (jak je wyliczysz ) Więc, że P₃ = P₄ ... więc P₃ = ...

Blee: Wiesz, że

salamandra: O matko....., wiedziałem, że muszę obliczyć pole jednego z nich, a później odjąć od pola trapezu, ale przecież moge już teraz odjąć i podzielić na dwa dzięki bardzo