trapezik
Komornik: Dane są trzy kolejne wierzchołki trapezu równoramiennego ABCD , gdzie BC jest jego dłuższą
podstawą, A(0,1,2), B(−1,−2,0), C(4,0,−1). Znajdź współrzędne wierzchołka D.
12 lut 12:50
Blee:
Metoda I (zalecana):
1) wyznaczasz długość ramienia AB
2) wyznaczasz równanie prostej równoległej do BC przechodzącej przez punkt A
3) wyznaczasz wzór okręgu o promieniu |AB| i środku w punkcie C
4) wyznaczasz punkty (dwa ... ewentualnie jeden − jeżeli ten trapez jest prostokątem)
przecięcia się prostej (2) z okręgiem (3).
Gotowe
12 lut 13:14
Komornik: Jak wyznaczyć to równanie okręgu w przestrzeni?
12 lut 14:01
Leszek: Lub wykorzystaj wektory :
BC = [ 5;2;−1]
BA= [ 1;3;2]
BD= BA+BC = [ 6;5;1]
Dokoncz !
12 lut 14:06
Blee:
Leszek ... no i co otrzymasz po tej sumie? Odpowiedź brzmi −−− jedno z rozwiązań (będziesz miał
równoległobok)
A co jeżeli CD nie jest równoległa do AB
Autorze ... wybacz ... nie zauważyłem że to przestrzeń
to zacznijmy od tego aby wyznaczyć płaszczyznę na której masz punktu A,B,C.
Później okrąg wyznaczasz z części wspólnej sfery i tejże właśnie płaszczyzny
12 lut 14:10
Leszek: Otrzymalem D( 5,3,1) oraz |AB| = |DC| = √14 , wiec chyba jest dobrze ?
12 lut 14:14
Blee:
chociaż wróć ...
a w dupie mamy okrąg ... wyznaczy sfera i ta prosta (do której i tak jest potrzebne równanie
płaszczyzny −−− tego nie przeskoczymy)
12 lut 14:14
Blee:
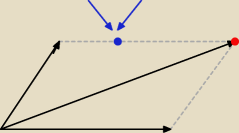
Leszek wyznaczyłeś
ten punkt
A co z
tym punktem
12 lut 14:16
Leszek: Wektory : AD= [ 5;2;−1] , AD II BC
12 lut 14:19
Leszek: Kolego Blee
Wektor BD = [ xD +1; yD +2; zD −0] czyli D( 5,3,1)
12 lut 14:21
Blee:
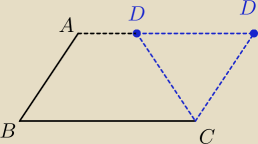
Leszek ... a od kiedy wektor AD i BC (w trapezie) mają zawsze te same długości
Oczywiście,
że są równoległe.
Ja nie przeczę że JEDNO rozwiązanie w ten sposób otrzymasz ... ale TYLKO jedno.
Obie te pozycje są prawidłowymi (spełniającymi warunki zadania) pozycjami punktu D ... Ty
robiąc sumę wektorów wyznaczasz tylko jeden (ten odpowiadający równoległobokowi)
12 lut 14:23
Leszek: Kolego Blee , masz racje wyznaczylem punkt D dla rownolegloboku !
12 lut 14:27
Leszek: Teraz z iloczynu skalarnego wyznaczam kat ABC = kat DCB ( chce znalezc prostsza metode ,
bez sfery , na wektorach w przestrzeni )
12 lut 14:32
Blee:
Leszek ... jeśli już na wektor chcesz to proponuję na przykład takie podejście:
1) wyznaczyć wektor prostopadły do BC i skalujemy jego długość tak aby:
BA + AE = BE (czyli AE jest wysokością)
2) robimy wektor CF równy −2BE
3) BC + CF + BA <−−− i masz drugi punkt D
Szczerze mówiąc ... to na ile łatwe będzie skalowanie długości wektora AE no i także
wyznaczenie prostopadłego wektora do BC (w końcu jesteśmy w przestrzeni)
12 lut 14:45
Blee:
miało być:
Szczerze mówiąc ... to nie wiem na ile ....
12 lut 14:49
Mila:
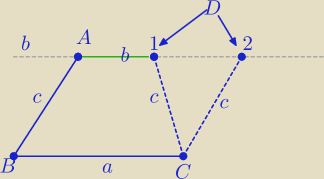
A(0,1,2), B(−1,−2,0), C(4,0,−1).
c.d.
Korzystając z Waszych obliczeń:
BC
→ = [ 5,2,−1]
BA
→= [ 1,3,2]
|AB|=
√14
Prosta AD:
AD||BC
k
→=[5,2,−1] wektor kierunkowy
x=5t
y=1+2t
z=2−t, t∊R
(x−4)
2+y
2+(z+1)
2=14 i x=5t, y=1+2t, z=2−t,
| | 9 | | 8 | |
D1=(2, |
| , |
| lub D2=(5,3,1) |
| | 5 | | 5 | |
12 lut 20:00
Komornik: Dzięki wam
12 lut 20:01
Mila:
12 lut 20:03
12 lut 20:43
Mila:
Dziękuję ślicznie, tak sobie narysowałam , ale na kartce nie można obracać
12 lut 22:11