najmniejsza wartosc funckji Gangster: Wykaz ze funkcja f(x)= x²−6x przyjmuje najmniejsza wartosc rowna −9 zadanie banalne, jednak jak to zrobic bez funckji kwadratowej? bez delty?

salamandra: Pochodna?

ABC: normalnie ze wzoru na (a−b)² x²−6x=(x−3)²−9 i koniec

janek191: f(x) = x² − 6 x

	6
p =		= 3
	2

y_min = q = f(3) = 3² − 6*3 = 9 − 18 = − 9

Saizou : zabierasz się za zadanie z funkcji kwadratowej i chcesz bez niej rozwiązać zadanie? Ciekawe x²−6x=x²−6x+9−9=(x−3)²−9 → wartość najmniejsza dla x=3

logika: Ramiona skierowane do góry → najmniejsza wartość funkcji jest w wierzchołku paraboli.

Gangster: dzieki Saizou, Co do reszty ludzie to jest funckja kwadratowa, umiem to policzyc za jej pomoca, ja chcialem zrobic to bez funkcji kwadratowej

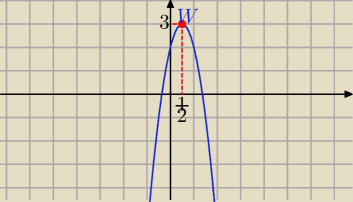
Gangster: a taka funkcja? f(x)= −4x²+4x+2 wykazac ze przyjmuje najwieksza wartosc rowna 3

a@b:

	4
xmax=xw=		=1/2
	8

f(1/2)= ......... = 3

Gangster: ale jest to funkcja kwadratowa a ja potrzebuje rozwiazania bez jej uzycia

a@b:

a@b: f(x)=−4(x−¹₂)²+3

logika: Nie, nie określiłeś się dokładnie. To co zrobił Saizou to również metoda zwijania funkcji kwadratowej do postaci kanonicznej. Czyli jest to postać kanoniczna funkcji kwadratowej. A więc wciąż coś związanego z funkcją kwadratową A licząc wierzchołek i wartość w wierzchołku masz to samo