stereometria
salamandra: Proszę o pomoc do ćwiczenia 29
https://imgur.com/a/ncZKJI4
Ustaliłem, że Q
1C
1 = 4, a D
1Q
1= 12
C
1R
1 = 4
więc Q
1R
1 = 4
√2
LK (przekątna podstawy?) = 16
√2
No i ja próbowałem z podobieństwa trójkątów wyznaczyć KR
1:
KR
1=12
√2
B
1R
1 = 12
z tw. Pitagorasa
(B
1K)
2+12
2 = (12
√2)
2
B
1K=12
B
1B=16
BK=4
| | 64 | |
W odpowiedzi jest jak widać− |
| |
| | 7 | |
11 lut 19:21
ite: Z podobieństwa których trójkątów?
LK nie jest przekątną podstawy (bo do niej nie należy) ale ma taką samą długość.
Do rozwiązania potrzebny jest przekrój płaszczyzną AA1CC1.
11 lut 19:42
salamandra: Miałem na myśli podobieństwo trójkątów KB1R1 i BB1C1
11 lut 19:49
ite: ΔBB1C1 jest równoramienny, a czy ΔKB1R1 taki jest nie wiesz. Gdybyś to wykazał, to
odpowiedź |BK|=12 byłaby natychmiastowa.
11 lut 19:58
salamandra:
A kąty w nich nie będą takie same? to tak nie działa jak myślę>?
11 lut 20:00
ite:
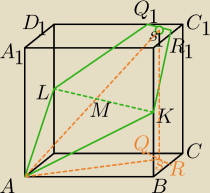
spójrz na ten rysunek
11 lut 20:07
ite: 20:00 α=β=45o więc ΔBB1C1 jest równoramienny
11 lut 20:11
salamandra: Kiepsko widzę, to pomarańczowe to trójkąt?
11 lut 20:11
salamandra: Nie wiem niestety jak to zrobić, kompletna pustka
11 lut 20:24
11 lut 20:29
Mila:
ite niezawodna z Geogebrą.
11 lut 20:31
11 lut 20:35
ite:
11 lut 20:42
salamandra: W ogóle próbowałem ostatnio te geogebre, ale nie mogłem znaleźć jak figury przestrzenne
rysować, mogłem tylko wielokąty
11 lut 20:43
ite: musisz wybrać widok 3D
11 lut 20:58
salamandra: https://i.imgur.com/tEcR82w.jpg chodziło oczywiście o tę podpowiedź w przykładzie 15, nie skopiował mi się link,
potrzebuję pomocy teraz z ćwiczeniem 28.
Przekrój jest trapezem, którego pole = 54
√3
Bok FC=2*6=12
E
1D
1=6
54
√3=9h
h=6
√3
z tw. Pitagorasa.
6
2+H
2=(6
√3)
2
36+t
2=108
t
2=72
t= 6
√2
Co tu jest źle?
11 lut 22:09
salamandra: Nieważne, ja założyłem, że wysokość trapezu to będzie również jego krawędź boczna CD1. Już
wyszło.
11 lut 22:12
