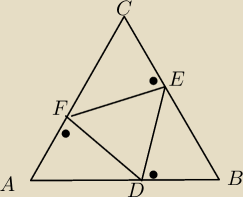
 Na bokach AB,BC,CA trójkąta równobocznego ABC wybrano kolejno punkty D,E,F tak, że DE ⊥ AB,
EF⊥BC i FD ⊥ AC.
Wykaż, że trójkąt DEF jest trójkątem równobocznym o polu trzy razy mniejszym od pola trójkąta
ABC
Zaraz zamieszczę rozwiązanie z rysunkiem
Na bokach AB,BC,CA trójkąta równobocznego ABC wybrano kolejno punkty D,E,F tak, że DE ⊥ AB,
EF⊥BC i FD ⊥ AC.
Wykaż, że trójkąt DEF jest trójkątem równobocznym o polu trzy razy mniejszym od pola trójkąta
ABC
Zaraz zamieszczę rozwiązanie z rysunkiem
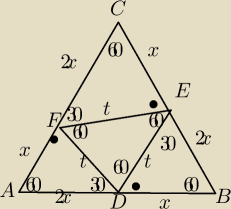 t=x√3
Czy mogę postąpić, jakby to było założenie, że DEF jest równoboczny?
wtedy z własności trójkąta 30,60,90 wiem, że AD = 2x, DB=x, FD=t=x√3, pozostałe analogicznie.
t=x√3
Czy mogę postąpić, jakby to było założenie, że DEF jest równoboczny?
wtedy z własności trójkąta 30,60,90 wiem, że AD = 2x, DB=x, FD=t=x√3, pozostałe analogicznie.
| (x√3)2√3 | 3x2√3 | |||
i wtedy PDEF= | = | |||
| 4 | 4 |
| 9x2√3 | ||
PABC= | ||
| 4 |
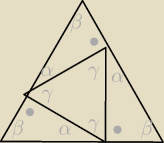 DEF jest równoboczny, ale trzeba to pokazac
DEF jest równoboczny, ale trzeba to pokazac  W sumie to zrobiłeś, ale na odwrót.
α=30
β=60
zatem γ=60
W sumie to zrobiłeś, ale na odwrót.
α=30
β=60
zatem γ=60
 Dzięki
Dzięki  Teraz mam zadanie:
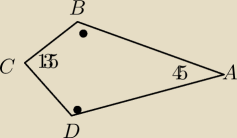
W czworokącie wypukłym ABCD dane sa kąty ADC=ABC= 90 oraz DCB=135. Wykaż, że
Teraz mam zadanie:
W czworokącie wypukłym ABCD dane sa kąty ADC=ABC= 90 oraz DCB=135. Wykaż, że
| DB | √2 | |||
= | ||||
| AC | 2 |

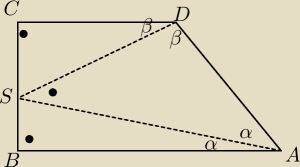 Teraz jasne dzięki
Teraz jasne dzięki  niejasne natomiast mam kolejne zadanie:
Dany jest trapez prostokątny ABCD o podstawach AB i CD, w którym boki AB i BC są prostopadłe.
Dwusieczne kątów A i D przecinają się w punkcie S leżącym na boku BC. Wykaż, że BS=SC
2β+90 = 180
β=45
2α+90=180
α=45
DSA=180−α−β = 90
ADS prostokątny.
I na tym utknąłem
niejasne natomiast mam kolejne zadanie:
Dany jest trapez prostokątny ABCD o podstawach AB i CD, w którym boki AB i BC są prostopadłe.
Dwusieczne kątów A i D przecinają się w punkcie S leżącym na boku BC. Wykaż, że BS=SC
2β+90 = 180
β=45
2α+90=180
α=45
DSA=180−α−β = 90
ADS prostokątny.
I na tym utknąłem
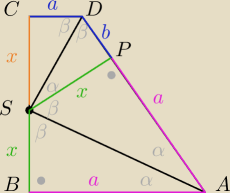 Nieprawdą jest że 2β+90=180 itd.
Z definicji dwusiecznej mamy, że |SB|=|SP|. ΔABS ≡ ΔAPS (kbk)
analogicznie ΔSCD ≡ ΔSPD
zatem...
Nieprawdą jest że 2β+90=180 itd.
Z definicji dwusiecznej mamy, że |SB|=|SP|. ΔABS ≡ ΔAPS (kbk)
analogicznie ΔSCD ≡ ΔSPD
zatem...
 tutaj masz, że suma miar kątów leżących przy jednym ramieniu wynosi 180
tutaj masz, że suma miar kątów leżących przy jednym ramieniu wynosi 180

