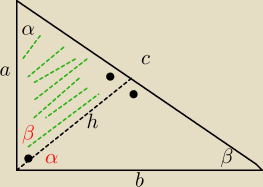
planimetria salamandra: Obwód trójkąta prostokątnego wynosi 60 cm, a tangens jednego z kątów ostrych jest równy

	5
		. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta
	12

prostego na przeciwprostokątną.

	b
tgα=
	a

5		b
	=
12		a

12b=5a

	12
a=		b
	5

	12
cosα=
	13

	12   b 5
cosα=
	c

12		12   b 5
	=
13		c

	156
12c=		b
	5

	13
c=		b
	5

12		13
	b+b+		b=60
5		5

6b=60 b=10 c=26 a=24 Z zielonego trójkąta:

	h
tgα=
	a

5		h
	=
12		a

5		h
	=
12		24

120=12h h=10.

	1
P=		*a*b*sin90 = 120
	2

Jest ok?

salamandra:

	h
Jeden błąd już widzę bodajże− z zielonego trójkąta sinα zamiast tgα to		i wyjdzie
	a

	120
h=
	13

Saizou : Ale utrudniasz sobie życie

	5
skoro tgα=		to przyprostokątne mają długości 5x oraz 12x.
	12

Doliczasz przeciwprostokątną i korzystasz z obwodu. Następnie pole na 2 sposoby i koniec

salamandra: powoli, ale do celu dzięki

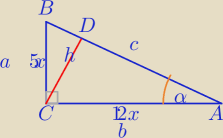Mila: Nieco krócej:

	5
tgα=
	12

x− wspólna miara a=5x, b=12x 1) c²=25x²+144x² ⇔c=13x 5x+12x+13x=60 30x=60 ⇔x=2 a=10cm, b=24cm, c=26cm

	1
2) PΔ=		*10*24⇔P=120cm2
	2

	1		240
120=		*26*h ⇔h=
	2		26

	120
h=		cm
	13

==============