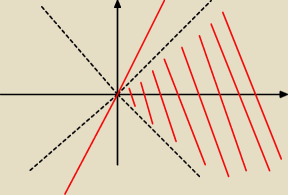
zbiór logika: Mam naszkicować zbiór {<x, y> ∊ R²: x <|y| ⇒ y = 4x} Wobec tego, najpierw rozpatrzmy, kiedy poprzednik jest prawdziwy i następnik również. Widać, że prosta y = 4x zawiera się w tej części płaszczyzny, którą wyznacza x < |y|. Wobec tego zarówno poprzednik jak i następnik są prawdziwi tylko wtedy, gdy y = 4x. Z kolei jeśli x > |y|, to następnik może być dowolny. Czy wobec tego będzie to zbiór, który zaznaczyłem na rysunku? Legenda: przerywane linie − proste y = x oraz y = − x czerwona prosta − prosta y = 4x

ite: Trochę inny zbiór. Najwygodniej skorzystać z prawa eliminacji implikacji i podany warunek zamiast (p ⇒ q) zapisać w postaci (~p ∨ q). Wtedy rysujesz sumę dwóch obszarów. Zaprzeczenie (x <|y|) jest inne niż podajesz.

logika: Faktycznie. ¬(x < y ∧ −x > y) ⇔ x ≥ y ∨ −x ≤ y. Zaraz spróbuję poprawić

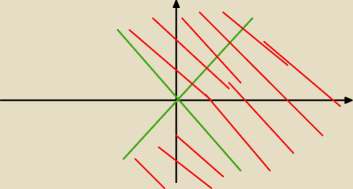
logika: Czyli to będzie czerwony obszar + te dwie zielone proste. Bo to będzie suma zbiorów x ≥ y, −x ≤ y oraz 4x = y

ite: (x <|y|) to nie to samo co (x < y ∧ −x > y) (x <|y|)⇔(x < y ∨ −x > y) chyba prościej ¬(x<|y|) zapisać (x≥|y|) ten poprzedni obszar + półproste wyznaczające go, ponieważ warukiem jest nie x>|y| ale x≥|y|

Bez komentarza: Dobra, faktycznie, ten mój warunek jest głupi. Dziękuję za pomoc