Wartość bezwględna York: Cześć, Mam naszkicować wykres funkcji f(x) = x|x−4| Czy mogę moduł wymnożyć przez x? Bo wiem, że gdyby to była liczba to mogę liczbę wymnażać przez moduł, ale nie wiem jak ze zmienną.

Blee: rozpatrz dwa przypadki: x ≥ 4 wtedy f(x) = x*(x−4) x < 4 wtedy f(x) = x*(−(x−4)) = −x*(x−4) i rysujesz

York: OK, dzięki

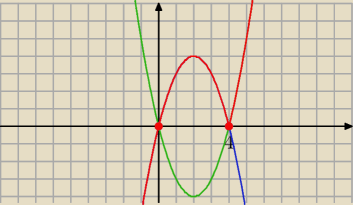
a@b: 1/ dla x <4 f(x)= x( −x+4) = −x²+4x −− część paraboli 2/ dla x≥4 f(x)= x(x−4) x²−4x −−− część paraboli f(x) −−− czerwony wykres

York: A jeszcze drugie pytanie, jeśli mam rozwiązać równanie gdzie mam tylko dwie wartości bewzględne np.: |3x−1 = |4x+5| to tutaj mogę sobie podnieść do kwadratu i wyjdzie mi jakaś funkcja kwadratowa, ale jeśli miałbym dodatkowo liczbę w równaniu np. |3x−1 = |4x+5| + 7 to tutaj nie opłaca się chyba podnosić do ² tylko rozwiązywać przedziałami, prawda?

Blee: niee ... wtedy rozpatrujesz 3 przypadki Nie podnosisz do ²

PW: Dla równania |3x − 1| = |4x + 5| myślenie jest następujące: |a| = |b| ⇔ (a = b) ∨ (a = − b), a więc rozpatrywane równanie jest równoważne alternatywie równań 3x − 1 = 4x + 5 ∨ 3x − 1 = 4x + 5.

PW: Oczywiście drugie rónanie powinno wyglądać: 3x − 1 = − (4x + 5)