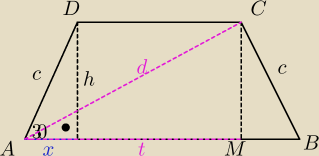
planimetria salamandra: Pole trapezu równoramiennego jest równe 39√3. Ramię długości 6√3 tworzy z dłuższą podstawą kąt o mierze 30 stopni. Oblicz obwód L trapezu i długość d przekątnej trapezu. c=6√3

	a−b
x=		, gdzie a= długość dłuższej podstawy, b= długość krótszej podstawy
	2

	a+b
t=
	2

sin30 = U{h}{6√3 h=3√3

	h
tg30=
	x

√3		3√3
	=
3		x

x=9

	(a+b)*3√3
P=
	2

	(a+b)*3√3
39√3=		/ *2
	2

78√3=(a+b)*3√3 a+b=26

a+b
	= 13
2

t=13 z tw. cosinusów w ΔAMC d²=13²+(3√3)²−2*13*3√3*cos90 d²=169+27 d²=196 d=14

	a+b		a−b
b=		−(		)= 4
	2		2

a=22 L=26+12√3 Czy jest jakiś prostszy sposób na to zadanie, którego nie znam, gdyż ten sposób jest trochę czasochłonny. Z góry dzięki za ewentualne alternatywy

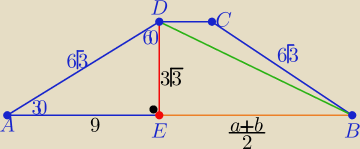a@b: 1/ z trójkata AED"ekierki" : h=3√3, |AE|=9

	a+b
W trójkącie EBD : |EB|=
	2

	a+b
P=		*3√3 ⇒ a+b=26
	2

L=12√3+26 ========== i po ptokach

a@b: Oblicz jeszcze : |BD|² =h²+|EB|² |BD|=..........

salamandra:

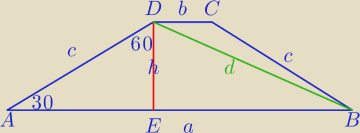Mila: P=39√3 c=6√3

	a+b		a−b
W trapezie równoramiennym : |EB|=		, |AE|=
	2		2

=================================================== 1) W ΔAED: h=3√3

	a+b
39√3=		*3√3
	2

a+b
	=13
2

a+b=26 2) W ΔDEB: d²=13²+(3√3)² d=14 3) L=26+12√3 d=14

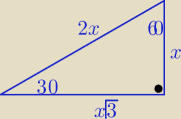a@b: Trójkąt "ekierkowy" o kątach 30^o,60^o, 90^o

salamandra: Dziękuję Wam, zawsze to te dwie minuty zaoszczędzone na maturze