| a+b | sinα+sinβ | |||
że w trójkącie tym prawdziwy jest związek | = | |||
| b | sinβ |
| a | b | ||
= | |||
| sinα | sinβ |
| b*sinα | ||
a= | ||
| sinβ |
| a*sinβ | ||
b= | ||
| sinα |
| |||||||||||||
= | |||||||||||||
|
| ||||||||
= | ||||||||
|
| ||||||||
= | = | |||||||
|
| b*sin2α+a*sin2β | sinα | |||
* | , | |||
| sinβ*sinα | a*sinβ |
| a+b | a | ||
= | +1 | ||
| b | b |
| a | b | a | sinα | ||||
= | → | = | |||||
| sinα | sinβ | b | sinβ |

 A z tego mojego idzie coś na sile wyskrobać?
A z tego mojego idzie coś na sile wyskrobać?
 Za bardzo skomplikowałeś, nie możesz wyrażać a i b za pomocą a i b.
Stosujesz zasadę ignotum per ignotum.
===========================
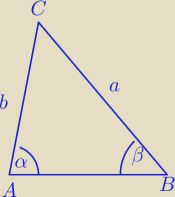
Z tw sinusów:
Za bardzo skomplikowałeś, nie możesz wyrażać a i b za pomocą a i b.
Stosujesz zasadę ignotum per ignotum.
===========================
Z tw sinusów:
| a | |
=2R⇔a=2R sinα | |
| sinα |
| b | |
=2R⇔ b=2R sinβ | |
| sinβ |
| a+b | 2R sinα+2R sinβ | ||
= | ⇔ | ||
| b | 2R sinβ |
| a+b | sinα+sinβ | ||
= | |||
| b | sinβ |
