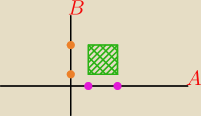
iloczyn kartezjański logika: (1) Niech A ⊆ X, B ⊆ Y . Zapisz (A × B)^c jako sumę iloczynów kartezjańskich. (2) Załóżmy, że A, B, C i D są niepustymi zbiorami: (a) Czy z tego, że (A × B) ⊆ (C × D) wynika, że A ⊆ C i B ⊆ D? (b) Pokaż, że jeśli A × B = C × D, to A = C i B = D. (c) Czy z tego, że (A × B) ∩ (C × D) = ∅ wynika, że A ∩ C = ∅ i B ∩ D = ∅? W (1) zacząłem od skonstruowania przykładowego rysunku. Wynika z niego, że: (A × B)^c = ((X\A) × Y) ∪ (A × (Y\B)) (2) Zacznijmy od (a): Wiemy, że (A × B) ⊆ (C × D). Weźmy w takim razie dowolną parę uporządkowaną <a, b> ∊ A × B. Skoro (A × B) ⊆ (C × D), to <a, b> ∊ C × D. W takim razie wiemy, że a ∊ A i a ∊ C oraz b ∊ B i b ∊ D. Skoro wzięliśmy dowolną parę uporządkowaną, to elementy tworzące tę parę są dowolne. Więc widzimy, że dowolny element a ∊ A należy do C, tak samo dowolny element b ∊ B należy do D. Wobec tego wiemy, że jeśli a ∊ A ⇒ a ∊ C. A to jest równoważne temu, że A ⊆ C. Analogicznie B ⊆ D. Teraz spróbujmy (b): Skoro A × B = C × D, to z zasady ekstensjonalności wiemy, że oba zbiory mają tyle samo dokładnie takich samych elementów. W takim razie każda para uporządkowana <a, b> ∊ A × B również należy do zbioru C × D. Wobec tego wiemy, że dowolne a ∊ A również należy do C, więc A = C. Analogicznie druga równość. I na koniec (c): (A × B) ∩ (C × D) = {<a, b>: a ∊ A ∧ b ∊ B ∧ a ∊ C ∧ b ∊ D} = {<a, b>: a ∊ (A ∧ C) ∧ b ∊ (B ∧ D)}. No więc skoro {<a, b>: a ∊ (A ∧ C) ∧ b ∊ (B ∧ D)} = ∅, to chyba musi zajść A ∩ C = B ∩ D = ∅, bo znowu powołując się na zasadę ekstensjonalności: dwa zbiory są równe, gdy elementy zbiorów są równe. Ale w zbiorze pustym nie mamy żadnych elementów, więc w zbiorze po lewej stronie również nie możemy mieć żadnych elementów. Wobec tego jeśli A ∩ C = ∅, to a ∉ A ∩ C. Analogicznie dla zmiennej b. Będę wdzięczny za sprawdzenie i wytknięcie błędów

ite: (c) Czy z tego, że (A × B) ∩ (C × D) = ∅ wynika, że A ∩ C = ∅ i B ∩ D = ∅? Sprawdź dla A={1,2}, C={2,3}, B={♠}, D={♦}.

ite: (1) (A × B)^c = ((X\A) × Y) ∪ (X × (Y\B)) = (A^c × Y) ∪ (X × B^c)

logika: Co do (1), czemu bierzemy X? Chodzi o to, by nie wykorzystać A? Czy może jednak rysunek wprowadza w błąd? Bo ja to widzę tak, że: ((X\A) × Y) − ten zbiór to zbiór elementów, w których pierwsza współrzędna z pewnością nie należy do zbioru A. Z kolei w drugim zbiorze widzę to tak, że na pierwszej współrzędnej mam elementy należące do A, ale za to na drugiej współrzędnej mam elementy, które nie należą do B.

logika: Co do (c): A × B = {<1, ♠>, <2, ♠>} C × D = {<2, ♦>, <2, ♦>} No i tutaj część wspólna będzie pusta, a zbiory nie bardzo, więc dowód do bani. Można prosić o jakiś jego szkic lub pomysł?

logika: Hm, więc tak nieśmiało wnioskując, to wystarczy, by tylko jeden z przekrojów był pusty?

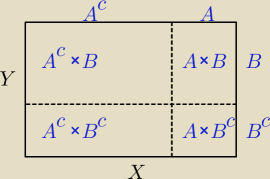
ite: 20:54 OK, jak narysowałam rysunek "po swojemu", to już widzę, że obie sumy są równe. (A^c × Y) ∪ (X × B^c)=((X\A) × Y) ∪ (A × (Y\B))

ite: (c) Wystarczy podanie jednego kontrprzykladu, żeby wykazać, że takie twierdzenie nie jest prawdziwe.

logika: (c) Wiem, tylko jak widzisz: nie widziałem, że jest to fałszywe. Więc ciężko, bym wymyślał kontrprzykład próbując udowodnić coś, co prawdziwe nie jest

logika: A co z (a) oraz (b)?

ite: Nie rozumiem zapisów w (c) ale podejrzewam, że 19:50 nie wziąłeś pod uwagę praw de Morgana.

logika: Tam pod koniec w (c) chodziło mi o to, że gdyby a ∊ A ∩ C oraz A ∩ C = ∅, to wtedy a ∊ ∅. I to w sumie daje sprzeczność.

ite: 21:21 dobry pomysł a i b przemyślę już jutro

logika: Okej, bardzo dziękuję za Twój czas poświęcony tutaj