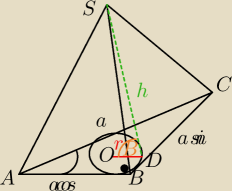
stereometria asd: Nie prosze o rozwiazanie,tylko naprowadzenie czy moj sposob jest ok Podstawa ostrosłupa jest trójkat prostokatny o kacie ostrym α i przeciwprostokatnej długosci a. Wszystkie sciany boczne ostrosłupa sa nachylone do płaszczyzny podstawy pod katem β.Wykaz, ze

	a2sin2α(cosβ+1)
pole powierzchni całkowitej tego ostrosłupa jest rowne
	4cosβ

Powiedzmy,ze ten okrag jest wpisany. Niech ∡BAC = α Po zastosowaniu zaleznosci na sin i cos w ΔABC AB = acosα BC = asinα

	asinα+acosα−a
Wiec r okregu wpisanego w ten trojkat bedzie wynosilo r =
	2

I z ΔSOD np z zaleznosci cosβ wyznaczam h w ΔBCS,analogicznie do reszty scian bocznych?

Blee: Tak ... Zauważ także, że każda ze ścian bocznych będzie miała taką samą wysokość

asd: dziekuje