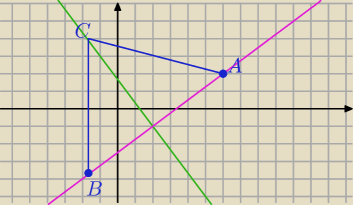
 zielona prosta to ta podana w poleceniu
rozowa prosta to prosta prostopadla do zielonej przechodzaca przez punkt A
(to na niej leza punkty A i B)
wiec przykladowy rysunek to taki
zielona prosta to ta podana w poleceniu
rozowa prosta to prosta prostopadla do zielonej przechodzaca przez punkt A
(to na niej leza punkty A i B)
wiec przykladowy rysunek to taki
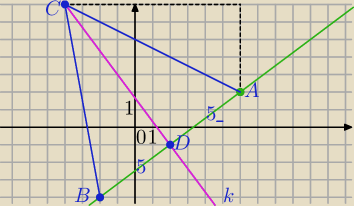 1) A=(6,2)
2) k: 4x + 3y − 5 = 0
1) A=(6,2)
2) k: 4x + 3y − 5 = 0
| 4 | 5 | |||
y=− | x+ | |||
| 3 | 3 |
| 3 | 3 | 5 | ||||
y= | x +b i 2= | *6+b, b=− | ||||
| 4 | 4 | 2 |
| 3 | 5 | |||
AB: y= | x− | |||
| 4 | 2 |
| 4 | 5 | 3 | 5 | |||||
− | x+ | = | x− | |||||
| 3 | 3 | 4 | 2 |
| 4 | 5 | |||
(x−2)2+(y+1)2=102 i y=− | x+ | ⇔ | ||
| 3 | 3 |
| 4 | 8 | |||
x2−4x+4+(− | x+ | )2=100 | ||
| 3 | 3 |
| 5(√5−1) | ||
r= | − promień okręgu wpisanego | |
| 2 |
| abc | ||
P= | ||
| 4R |
| a*b*c | ||
50= | ||
| 4R |
| 25 | ||
R= | ||
| 4 |