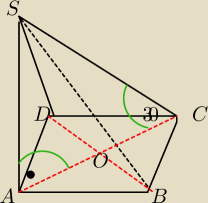
stereometria salamandra: Podstawą ostrosłupa jest romb o polu 144 cm², w którym stosunek długości przekątnych jest równy 2 :1. jedna z krawędzi bocznej ostrosłupa poprowadzono z wierzchołka kata ostrego rombu jest prostopadła do płaszczyzny podstawy. najdłuższa z krawędzi bocznych jest nachylona do płaszczyzny podstawy pod katem o mierze 30 stopni. oblicz: a) długość wszystkich krawędzi ostrosłupa b) objętość ostrosłupa Zacząłem od objętości, która powinna wyjść 480√3, a mi wychodzi 384√3 |AC|=2*|BD| |AC|=2x |BD|=x

	2x*x
P=
	2

	2x2
144=
	2

x²=144 x=12 Przekątne: 12, 24 ΔASC prostokątny (i tu przy okazji pytanie na potwierdzenie tezy, którą mi podała ostatnio Mila − każdy odcinek poprowadzony z punktu A byłby prostopadły do podstawy tak?)

	H
tg30=		(H=|AS|)
	24

√3		H
	=
3		24

24√3=3H H=8√3

	1
V=		Pp*H
	3

	1
V=		*144*8√3
	3

V=48*8√3 = 384√3, gdzieś mam błąd?

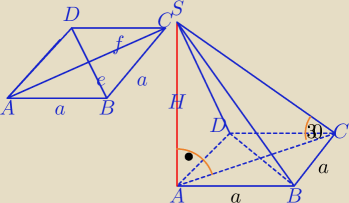Mila: 1) f=2e, α=30⁰ P_ABCD=144

	e*2e
144=
	2

144=e² e=12 f=24 a²=6²+12²=180 a=6√5 2)H=SA⊥do płaszczyzny podstawy⇒AC⊥H ΔSAC,ΔSAB, ΔSAD− Δprostokątne |AC| =24>a Dobrze pole obliczone, sprawdź w odpowiedzi długości krawędzi.

salamandra: a=6√5, AS=8√3, BS=DS=2√93, CS= 16√3. Krawedzie mi wyszły poprawnie, zgodnie z odpowiedzią, jednak nie wiem co z ta objętością

Mila: V − jest dobrze.

salamandra: Czyli błąd w odpowiedzi?