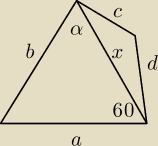
tw.cosinusów janusz: a=7,5 b=5√3 c=6 d=13,5−5√3 sinα=3/4 Mam obliczyć x,niby proste ale ciekawi mnie dlaczego gdy obliczę cosα i policzę w ten sposób: a²=b²+x²−2bxcosα

	5√21+15		5√21−15
Wychodzą dwie odpowiedzi x1=		i x2=		, ale w odp mam tylko x1.
	4		4

Czy x2 nie należy do jakiejś dziedziny? Sprawdzałem czy te dwa trójkąty mogą istnieć z x2 i wyszło że mogą. I tak wiem, że można to było policzyć prościej po prostu ciekawi mnie ten x2.

lola456: Druga odpowiedź bierze się stąd, że wyszły Ci dwa kąty dla cos i musisz wybrać jeden który spełnia warunki zadania.

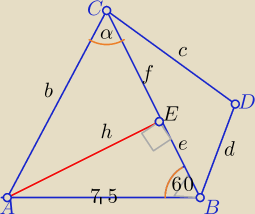
Mila: 1)

	7.5		15
W ΔAEB: e=		=3.75=
	2		4

	7.5√3		15√3
h=		=
	2		4

2) 5√3>7.5 (25*3=75>56.25) Stąd wniosek, że α<60⇔ α jest kątem ostrym.

	f
W ΔAEC: cosα=		, cosα>0
	b

	3
sinα=
	4

	9
cos2α=1−
	16

	√7
cosα=
	4

√7		f
	=
4		5√3

	5√21
f=
	4

3)

	15		5√21
|BC|=		+
	4		4

	15+5√21
|BC|=
	4

================= 5√3>7.5 (25*3=75>56.25) Stąd wniosek, że α<60⇔ α jest kątem ostrym. x>e=3.75