dowód z geometrii Heniu: W trójkącie o bokach długości a,b,c poprowadzono odcinki długości x,y,z styczne do okręgu wpisanego w ten trójkąt, mające końce na bokach trójkąta i równoległe odpowiednio do boków

	x		y		z
a,b,c . Wykaż, że		+		+		=1
	a		b		c

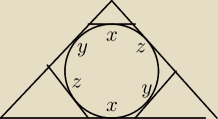
jc: Równoległe boki sześciokąta są równe (dlaczego?). Odcięte trójkąty są podobne do dużego trójkąta. Skala łatwa do odczytania. Podstawa jest sumą 3 odcinków.

	z		y
a = x + a*		+ b*
	c		b

	x		y		z
Stąd 1=		+		+		.
	a		b		c

Heniu: Nie rozumiem za bardzo

jc: Mała pomyłka − zamiast b* ... powinno być a*... Spójrz na lewy. trójkąt. Jest podobny do dużego trójkąta, tylko prawy bok ma długość z zamiast c. Wszystkie bogi są zmniejszone w skali z/c, a więc dolny bok ma długość az/c. Podobnie z prawym trójkątem. Pozostaje pytanie w nawiasie. Dlaczego odcinek pomiędzy małymi trójkątami ma długość równą długości podstawy górnego trójkąta?

Heniu: Dzięki Teraz rozumiem

Heniu: Jeszcze czegoś nie zrozumiałem i nie wiem jak jest z tymi bokami sześciokąta

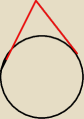
jc: Przeciwległe kąty sześciokąta są równe. Czerwone odcinki są równe. Wykorzystaj te dwa fakty. Inny sposób: obróć trójkąt o 180 wokół środka okręgu. Sobaczysz gwiazdę Dawida. Dalej może coś wypatrzysz.

jc: Zobaczysz ... (cóż tamto słowo znaczy? słownik zaakceptował)