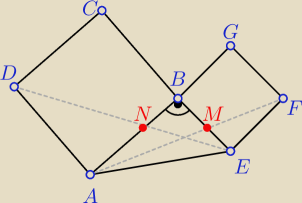
Planimetria abc: Do przyprostokatnych trojkata ABE dorysowano kwadraty (patrz rysunek). Nastepnie poprowadzono odcinek DE i w miejscu przeciecia tego odcinka z odcinkiem AB oznaczono punkt N. Analogicznie punkt M oznacza przeciecie sie odcinka AF z odcinkiem BE. Udowodnij, ze |BN| = |BM| Na poczatku planowalem narysowac te sytuacje w ukladzie wspolrzednych i wyznanczyc wszystkie punkty i proste itd ale wyglada na duzo roboty czy jest jakis inny sposob?

Blee: z podobieństwa trójkątów (albo jak wolisz to tw. Talesa)

|BN|		|BE|		|BE| * |CD|		|BE| * |CD|
	=		−> |BN| =		=
|CD|		|CE|		|CE|		|BC| + |BE|

oraz

|BM|		|AB|		|AB| * |GF|
	=		−> |BM| =
|GF|		|AG|		|AB| + |BG|

I teraz zauważ, że: |AB| = |BC| = |CD| = (oznaczmy to jako) a |BE| = |BG| = |GF| = (oznaczmy to jako) b więc mamy:

	b*a
|BN| =
	a + b

	a*b
|BM| =
	b + a

c.n.w.

abc: dziekuje