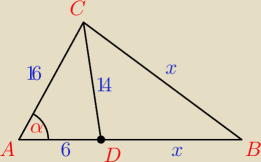
Trójkąt Szkolniak: Punkt D leży na boku AB trójkąta ABC oraz |AC|=16, |AD|=6, |CD|=14 i |BC|=|BD|. Oblicz obwód trójkąta ABC. x>0 z twierdzenia cosinusów w ΔADC:

	1
142=162+62−12*16*cosα ⇒ cosα=
	2

z twierdzenia cosinusów w ΔABC: x²=(x+6)²+16²−32(x+6)*cosα x²=x²+12x+36+256−16(x+6) 0=12x+292−16x−96 4x=196 ⇒ x=7 zatem obwód ΔABC równy jest 36. dobrze?

Leszek: Dobrze !

Szkolniak: super dzięki

Leszek: Ale : 4x = 196 ⇒ x= 49

Szkolniak: nie wiem czemu pierwiastek z tego wyciągnąłem w głowie, dzięki jeszcze raz