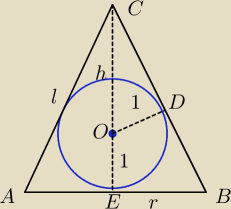
Stereometria - optymalizacja BoosterXS: W stożek wpisana jest kula o promieniu 1. Dla jakiej długości promienia podstawy tworząca tego stożka będzie najkrótsza? Stosuję oznaczenia, R−promień kuli, r−promień podstawy stożka, h−wysokość stożka, l−tworząca stożka, p − połowa obwodu trójkąta będącego przekrojem osiowym stożka. Po przyrównaniu 2 wzorów na pole trójkąta(będącego przekrojem stożka) i podstawieniu R=1 otrzymuję:

ah		r+l
	=rp ⇒ h=
2		r

z tw. Pitagorasa otrzymuję h²+r²=l² za h mogę podstawić to otrzymane z równania wyżej, ale wciąż mam w równaniu 2 niewiadome. Nie wiem jak z tym dalej ruszyć, jakieś podobieństwo trójkątów wewnątrz stożka i kuli? Zechce ktoś naprowadzić?

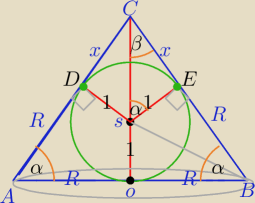
ite: ΔCEB∼ΔCDO stąd mamy układ równań

|CO|		|CB|
	=
|OD|		|EB|

oraz |CB|²=|CE|²+|EB|²

ite: Nie korzystam z tej połowy obwodu trójkąta będącego przekrojem osiowym stożka.

jc: Na to samo wychodzi. Teraz wyznaczasz h i wstawiasz do drugiego równania. No i się komplikuje. L spełnia równanie kwadratowe (współczynniki zależą do r).

jc: Nie jest tak źle.

	r+r3
L=
	r2−1

jc: Minimum mamy dla r=√2+√5. Chyba jednak coś pomyliłem?

jc: Jest jednak gorzej. Zamiast 1 wpisuję a. (L²−r²)r²=h²r²=a²(r+L)² (r²−a²)L² − 2a²rL − r²(r²+a²)=0

jc: Znów źle

jc: Jednak wcześniej było dobrze.

jc: Δ=4r⁶

	a2r+r3
L=
	r2−a2

Mila: 22:34 dobry wzór , wynik też.

a@b: Też tak mam

	r(r2+1)
L=
	r2−1

BoosterXS: Wciąż nie złapałem skąd wzór z 22:34

|CO|		|CB|		h−1		L		L
	=		⇒		=		⇒ h=		+ 1
|OD|		|EB|		1		r		r

Z Pitagorasa mamy: L²=h² + r² ⇒

	L
L2=(		+ 1 ) 2 + r2 ⇒
	r

	L2		2L
L2=		+		+ 1 +r2 /* r2?
	r2		r

L²r² = L² + 2Lr + r² + r⁴ no i tutaj się gubię, robię prawidłowo?

Mila: 1)

	α		1
W ΔBOS: tg		=
	2		R

	x
2) W ΔCES: tgα=		⇔
	1

	α   2tg   2		1   2*   R		2R
x= tgα=		⇔ x=		=
	α   1−tg2   2		1   1−   R2		R2−1

x>0,R>1 l(R)=x+R

	2R
l(R)=		+R
	R2−1

	R4−4R2−1
l'(R)=
	(R2−1)

itd