calki mat: Obliczyc calke ∫₀¹ ∫_x^√2−x2 x⁴−y⁴ dydx. Mozna zastosowac wspolrzedne biegunowe, ale po jakim obszarze calkowania to jest?

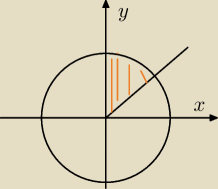
jc: Okrąg ma promień = √2.

jc: ∫_π/4^π/2 dφ ∫₀^√2 cos 2φ r³ dr = ...

mat: Czyli 0≤r≤√2 π/4≤φ≤π/2 x⁴−y⁴=r⁴cos⁴φ−r⁴sinφ=r⁴cos2φ Ale jak pomnoze przez jakobian rowny r, to mam r⁵cos2φ. Dlaczego tam jest r³?

jc: Oczywiście r⁵ Pomyliłem się.

mat: Ok. A czy ma znaczenie tutaj kolejnosc calkowania? Czy moge napisac tak: ∫₀^√2 ∫_π/4^π/2 cos2φ r⁵ dφ dr ?

jc: W tym zadaniu jest jeszcze lepiej, mnożysz osobno policzone całki (pomyśl dlaczego).

mat: To, ze φ jest do π/2 to widze, ale, ze od π/4 to nie bardzo. Czy da sie obliczyc, ze to jest akurat od π/4?

jc: Popatrz na rysunek.

mat: obliczam ∫₀^√2 ∫_π/4^π/2 cos2φ r⁵ dφ dr Ale ∫_π/4^π/2 cos2φ r⁵ dφ =−1/2r⁵ i pozniej ujemna wartosc a ujemna nie moze byc. dlaczego tak wychodzi?

jc: Masz przecież x≤y≤√2−x². Dlatego x⁴−y⁴≤0 i całka jest ujemna.

Mariusz: Czy przejście na układ biegunowy coś daje ? ∫₀¹ ∫_x^√2−x2 x⁴−y⁴ dydx.

	1
∫01 (x4y−		y5)|x√2−x2dx
	5

	1
∫01((x4√2−x2−		(2−x2)2√2−x2))dx
	5

	1
∫01		(5x4−(x4−4x2+4)√2−x2−4x5)dx
	5

	4		4
∫01		(x4+x2−1)√2−x2dx−∫01		x5dx
	5		5

	4		2
∫01		(x4+x2−1)√2−x2dx−
	5		15

4		2
	∫01(x4+x2−1)√2−x2dx−
5		15

	(x4+x2−1)(2−x2)
∫		dx
	√2−x2

	−x6+x4+3x2−2
∫		dx
	√2−x2

	x6		x4		x2		dx
−∫		dx+∫		dx+3∫		dx−2∫
	√2−x2		√2−x2		√2−x2		√2−x2

	xn		(−x)
∫		dx=∫(−xn−1)		dx
	√a2−x2		√a2−x2

=−xⁿ⁻¹√a²−x²+(n−1)∫xⁿ⁻²√a²−x²dx

	xn		xn−2(a2−x2)
∫		dx=−xn−1√a2−x2+(n−1)∫		dx
	√a2−x2		√a2−x2

	xn		xn−2
∫		dx=−xn−1√a2−x2+(n−1)a2∫		dx−
	√a2−x2		√a2−x2

	xn
(n−1)∫		dx
	√a2−x2

	xn		xn−2
n∫		dx=−xn−1√a2−x2+(n−1)a2∫		dx
	√a2−x2		√a2−x2

	xn		1		n−1		xn−2
∫		dx=−		xn−1√a2−x2+a2		∫		dx
	√a2−x2		n		n		√a2−x2

	1		5		x4
−(−		x5√2−x2+		∫		dx)
	6		3		√2−x2

1		5		x4
	x5√2−x2−		∫		dx
6		3		√2−x2

1		2		1		3		x2
	x5√2−x2−		(−		x3√2−x2+		∫		dx)
6		3		4		2		√2−x2

1		1		x2
	x5√2−x2+		x3√2−x2+2∫
6		6		√2−x2

1		1		1		dx
	x5√2−x2+		x3√2−x2+2(−		x√2−x2+∫		)
6		6		2		√2−x2

1		1		dx		dx
	x5√2−x2+		x3√2−x2−x√2−x2+2∫		−2∫
6		6		√2−x2		√2−x2

	1
∫(x4+x2−1)√2−x2dx=		(x5+x3−6x)√2−x2
	6

4		2		2
	(−		)−
5		3		15

	8		2
=−		−
	15		15

	10
=−
	15

	2
=−
	3

Tutaj pozwoliłem sobie wyprowadzić wzór redukcyjny i z niego skorzystałem Po zamianie zmiennych i tak trzeba będzie liczyć kilka razy przez części