planimetria jey:): Planimetria Z jednego brzegu jeziora widać szczyt góry pod kontem 18 stopni wzgledem poziomu z drugiego zas brzegu oddalonego od pierwszego o 1180 m w kierunku podnoza gory widac jej szczyt pod katem 22 stopni wzglegem poziomu. oblicz wysokosc h gory (mierzony wzgledem tafli wody) a nastepnie podaj wynik z dokladnoscia do 10m

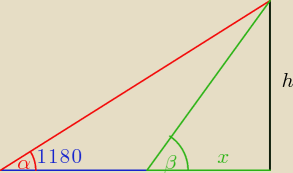
Godzio: α=18^o β=22^o

	h
tg18 =
	1180+x

	h
tg22 =
	x

tg18 ≈ 0,32 tg22 ≈ 0,4 377,6 + 0,32x = h 0,4x = h /* 0,8 377,6 + 0,32x = h 0,32x = 0,8h − −−−−−−−−−−−−−−−−−−−−−−−−−−−−− 377,6 = 0,2h h = 1888m

jey:): tu jest gdzieś błąd bo powinnobyc tak h=1180tg18tg22/tg22−tg18 = 1960

tim: Godzio zrobił, źle, że zaokrąglił.

tim: Pokazuję.

Godzio: mozna i tak :

	h
x =
	tg22

i z drugiego 1180 * tg18 + tg18x = h

	h−1180tg18
x =
	tg18

h−1180tg18		h
	=
tg18		tg22

tg22 * h − 1180 * tg18*tg22 = tg18 tg22 * h − tg18 * h = 1180 * tg18*tg22 h(tg22−tg18) = 1180 * tg18*tg22

	1180*tg18 *tg22
h =		= 1958,19 = 1958
	tg22−tg18

pewnie gdzieś źle przemnożyłem albo coś

tim:

	h
tg 18 =		− > h = tg 18 (1180 + x)
	1180+x

	h		h
tg 22 =		− > x =
	x		tg 22

h = tg 18 * 1180 + tg 18 x

	h
h = tg 18 * 1180 + tg 18 *
	tg 22

	tg 18
h = tg 18 * 1180 +		h
	tg 22

	tg 18
h −		h = tg 18 * 1180
	tg 22

	tg 18		tg 22
h (1 −		) = tg 18 * 1180 (1 =		)
	tg 22		tg 22

	tg 22 − tg 18
h (		= tg 18 * 1180
	tg 22

	tg 18 * 1180
h =
	tg 22 − tg 18     tg 22

	tg 18 * 1180 * tg 22
h =		= ...
	tg 22 − tg18

AS: Wynik: 1958.2 m

Godzio: miało być do 10m więc 1960

jey:): wielkie dzieki

AS: Do licha ciężkiego − nie wprowadzajcie takich innowacji w pisowni matematycznej − może to Was w przyszłości drogo kosztować przy ocenie zadań. Chodzi mi o zapis jey 1180tg18tg22/tg22−tg18 Powinno być prawidłowo 1180tg18tg22/(tg22−tg18) 8/4 − 2 i 8/(4 − 2) to są dwie różne wartości

Basia:

	h
tg18 =
	1180+x

	h
tg22 =
	x

x*tg22 = h

	h
x =
	tg22

	h
tg18 =
	h   1180+ )   tg22

	h
tg18(1180+		) = h
	tg22

	h*tg18
1180*tg18+		= h /*tg22
	tg22

1180*tg18*tg22 +h*tg18=h*tg22 h*tg22 − h*tg18 = 1180*tg18*tg22

	1180*tg18*tg22
h =
	tg22−tg18

nie ma błędu, tylko Godzio nie doprowadzał do tej postaci teraz mamy

	1180*0,32*0,4
h=		=
	0,4−0,32

1180*0,32*0,4
	=
0,08

1180*0,32*40
	=
8

1180*0,32*5 = 1180*1,6 = 1888 nie mam pod ręką tablic, możliwe, że gdzieś w odczycie tg18 lub tg 22 jest błąd, albo zbyt mała dokładność, albo Ty masz błąd w odpowiedzi

Basia: znalazłam jakieś w internecie i jest tak jak podał Godzio

Basia: dokładnie tg18=0,3249 tg22=0,404 może jak podstawisz te wartości będzie dobrze