Pole ograniczone krzywymi Ola: Oblicz pole między dwoma krzywymi: x = y² y = 2 − x. Trochę się gubię w tym nadal.

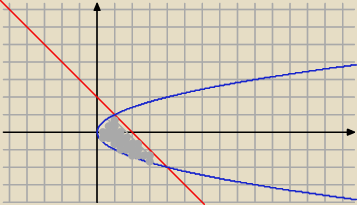
xyz: y² = x −−> y = √x lub y = −√x

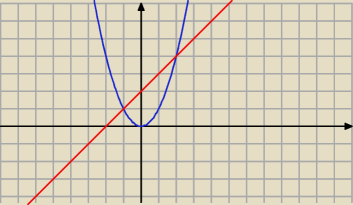
xyz: wiec jakby obrocic na normalny sposob to mamy

xyz: gdy sobie to obrocimy (rys. 2) to latwiej to policzysz (albo nie, w sumie nie wiem) bo pole to jest calka w granicach od a do b z funkcji od gory odjac funkcje od dolu wiec na rysunku 2 : 2 P = ∫ (x+2 − x²) dx = ... = 9/2 −1 Natomiast rys 1. to gdybys chciala granice dac po iksach to trzeba by bylo rozbic na dwa pola, pierwsze od 0 do 1, a drugie od 1 do 4, bo tylko jedna funkcja ograniczajaca od gory moze byc (i od dolu), dlatego lepiej granice po igrekach dac i wtedy y = 2−x −−> x = 2−y 1 P = ∫ (2−y − y²) = ... tez powinno wyjsc 9/2 −2

Ola: Dzięki A można to też rozpatrywać w ten drugi sposób, że rysujemy tak jakby wykresy iksów?

Ola: Trochę źle to ujęłam, ale w tym ostatnim komentarzu w sumie odpowiedziałeś na to pytanie, dzięki raz jeszcze.

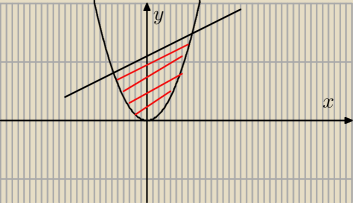
jc: Prosta przecina parabolę y=x² w punktach (a,a²) i (b,b²), a<b. Oblicz pole zaznaczonego fragmentu.