stereometria
salamandra: Zaznacz na rysunku:
a) kąt między przekątną BH, a krawędzią AB
b) kąt między przekątną CE, a przekątną podstawy AC
c) kąt między przekątną HC ściany, a przekątną EC graniastosłupa
Na razie chcę tylko pomocy do a), teoretycznie wiem gdzie będzie ten kąt, ale nie potrafię
sobie tego wyobrazić, że prowadzimy przekątną , a kąt w ogóle nie pokrywa się z tą przekątną.
Miałem to tłumaczone na zasadzie rzutu, że jak byśmy na przykład wyznaczali kąt między
przekątną ściany bocznej (dajmy na to, DG), a płaszcyzną podstawy, to punkt G' to będzie
dokładnie punkt C, a punkt D jest już na tej płaszczyźnie więc go nie obijamy, i tam gdzie G i
C to mamy kąt prosty, a przy D kąt α.
A w przypadku tego a), nie wiem jak mam sobie to "rzucić" proszę o wskazówkę
Mój rysunek:
https://imgur.com/a/rooaXRz
5 lut 19:36
Mila:
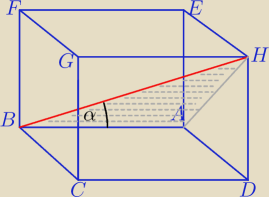
a)
5 lut 20:16
salamandra: To jest płaszczyzna Milu, tak? Kolokwialnie mówiąc − tak jakbym "płytę" tam przyłożył?
5 lut 20:18
Szkolniak: a) a gdybyś spróbował sobie wyobrazić widok tego z góry? może wtedy byłoby łatwiej?
5 lut 20:23
salamandra: Nie mam w ogóle wyobraźni przestrzennej, dlatego tak grzmiałem przed tym działem...., jeśli to
jest płaszczyzna, to co Mila napisała, to już będę kumał, bo ja to widziałem jako "gołe" kąty,
nie mające "domknięcia"
5 lut 20:25
Mila:
Zaraz będzie więcej objaśnień
5 lut 20:37
salamandra: 
5 lut 20:38
Mila:
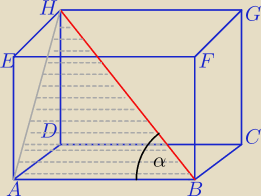
a)
5 lut 20:44
salamandra: A czy powstaje tam gdzieś kąt prosty? (w tej płaszczyźnie) Czy to nie jest w ogóle już rzut
prostokątny?
5 lut 20:46
Mila:
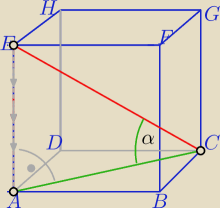
b) kąt między przekątną CE, a przekątną podstawy AC
5 lut 20:50
Mila:
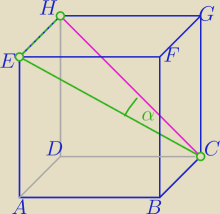
c) kąt między przekątną HC ściany, a przekątną EC graniastosłupa
Teraz napisz , gdzie jest kąt prosty w ΔHCE ?
5 lut 20:56
Mila:
Jako pomoc proponuję pudełko zapałek z usuniętą szufladką.
5 lut 20:57
Mila:
Gdzie jest kąt prosty w (a) w ΔABH ?
5 lut 20:58
salamandra: Zakładam, że HEC jest prosty, a w a) w ABH, HAB będzie prosty.
5 lut 21:00
Mila:
a) dobrze.
c) EH ⊥ ściany DCGH, zatem EH⊥HG, EH⊥HD i EH⊥HC
|∡EHC|=90o
5 lut 21:26
Mila:
Wyjaśnij teraz dlaczego kąt HAB będzie prosty.
5 lut 21:27
salamandra: Bo HA to jest tak jakby odcinek rzutujący?
5 lut 21:31
salamandra: I jest on prostopadły do rzutu?
5 lut 21:32
Mila:
AB⊥ściany bocznej ADHE, to AB jest prostopadły do AH.
5 lut 21:49
salamandra: Trochę tego nie rozumiem, to że AB jest prostopadłe do ściany bocznej− zgoda, to że AB jest
prostopadłe do załóżmy AE− zgoda, ale do AH? skąd to wynika, przecież to jest tak jakby
przekątna
5 lut 21:52
Mila:
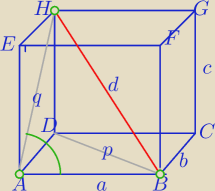
No to liczymy:
1) p
2=a
2+b
2
2) W ΔHDB: d
2=p
2+c
2=a
2+b
2+c
2⇔d=p[a
2+b
2+c
2}
3) W ΔADH: q
2=b
2+c
2
4) W ΔABH:
a
2+q
2=a
2+b
2+c
2 =
p2 z tw. odwrotnego do tw. Pitagorasa ⇒
ΔBAH jest trójkątem prostokątnym.
Narysuj na kartce pęk prostych. (za pomocą linijki )
Połóż kartkę na blacie biurka.
Postaw prostopadle ołówek w punkcie przecięcia tych prostych−
ołówek jest prostopadły do płaszczyzny biurka i do każdej z tych prostych.
5 lut 22:14
5 lut 22:22
Mila:
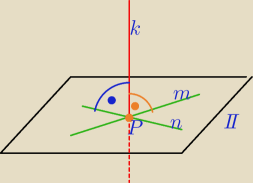
Jeżeli prosta przebija płaszczyznę i jest prostopadła do tej płaszczyzny ,
to jest prostopadła do każdej prostej przechodzącej przez punkt przebicia
i leżącej w tej płaszczyźnie.
k⊥π ⇒k⊥m i k⊥n
5 lut 22:30
salamandra: Ok, to założmy że EH lezy na prostej k. Jest ona prostopadła do płaszczyzny DCGH.
To w tym momencie H jest tym punktem "przebicia"?
5 lut 22:47
Mila:
Do którego rysunku się odnosisz?
5 lut 22:56
salamandra: 20:56
5 lut 23:00
Mila:
Tak, i przez punkt przebicia przechodzi prosta CH⇒CH⊥HE
5 lut 23:05
salamandra: A w przypadku 20:16 "A" jest punktem przebicia więc AH jest prostopadłe do AB?
5 lut 23:13
Mila:
tak.
5 lut 23:16
salamandra: chyba załapałem, ale nie obiecuję
dziękuję bardzo!
5 lut 23:16
5 lut 23:18
mogłabyś jeszcze zerknąć na to? byłbym wdzięczny https://matematykaszkolna.pl/forum/396842.html