całki ,pole ograniczone
hostessa: | | x | |
Pole obszaru ograniczonego osią OY I funkcjami y= |
| ,y=2−x,y=2 |
| | 2 | |
Pomocy nie wiem zupełnie jak się za to zabrać i jaka ma być całka oznaczona,z jakiego pola.
Narysowałam funkcje ale nie wiem którego obszaru pole mam policzyć:((
5 lut 12:15
Jerzy:
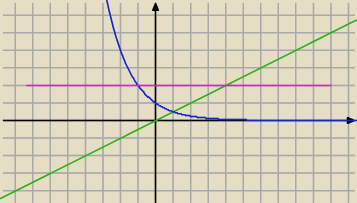
A teraz widzisz obszar ?
5 lut 12:19
hostessa: Dalej nie wiem który. Możesz zaznaczyć?
5 lut 12:20
Jerzy:
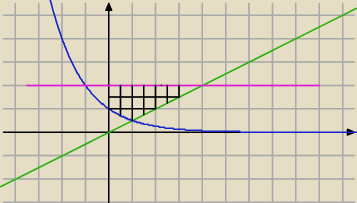
5 lut 12:23
piotr: ten "ograniczony": róż, niebo, zieleń.
5 lut 12:23
hostessa: A jak granice całkowania wyznaczyć?
5 lut 12:24
Jerzy:
Widać z wykresu: [0,1] i [1,4]
5 lut 12:25
Jerzy:
@piotr, jeszcze oś OY ogranicza ten obszar
5 lut 12:26
hostessa: | | x | |
Mi się wydaje że mam porównać wszystkie funkcje tzn. 2−x= |
| =2 tak? Czy osobno? |
| | 2 | |
5 lut 12:26
Jerzy:
| x | |
| = 2 oraz 2−x = 2 ⇔ x = 4 oraz x = 1 |
| 2 | |
5 lut 12:28
hostessa: Ok chciałam się upewnić dziękuję
5 lut 12:29
Jerzy:
Oczywiście 2
−x = 2 ⇔ x = −1 , ale nas ten punkt nie interesuje, bo oś OY ogranicza obszar.
| | x | |
Drugie równanie to |
| = 2−x ⇔ x = 1 |
| | 2 | |
5 lut 12:31
piotr: no to ten "ograniczony": róż, niebo, zieleń, czarnoziem
5 lut 12:31
hostessa: Dobrze a w takim razie funkcja ograniczająca Dolna i funkcja ograniczająca górna jak je
wyznaczyć?
5 lut 12:57
Jerzy:
Górna y = 2
Dolna 2−x (0,1) oraz x/2 (1,4)
5 lut 13:01
hostessa: | | 1 | |
Czyli całka od 0 do 1 dla f. y=2 I y=2−x oraz całka dla f.y= |
| x i y=2−x gdzie te |
| | 2 | |
pierwsze funkcje które napisałam są górnymi ograniczeniami tak?
5 lut 13:07
Jerzy:
| | x | |
Nie. ∫(2 − 2−x)dx + ∫(2 − |
| )dx |
| | 2 | |
5 lut 13:14
hostessa: Dziękuję

5 lut 13:48
 A teraz widzisz obszar ?
A teraz widzisz obszar ?

