prawdopodobienstwo Amelia: Wykaż, że jeśli P(A|B) = P(A|B′), gdzie P(B) > 0 i P(B′) > 0, to zdarzenie A i B są niezależne. P(A∩B) = P(A∩B') P(B) P(B') P(A ∩ B’) = P(A) – P(A ∩ B) P(B’) = 1 – P(B) jak przekształcić do tej postaci? P(A ∩ B) = P(A)P(B)

Saizou :

P(A∩B)		P(A∩B')
	=
P(B)		P(B')

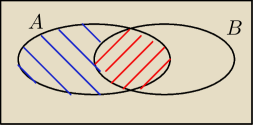
P(A∩B)*P(B')=P(A∩B')*P(B) P(A∩B)*(1−P(B))=P(A∩B')*P(B) P(A∩B)−P(B)*P(A∩B)=P(A∩B')*P(B) P(A∩B)=P(B)(P(A∩B)+P(A∩B')) P(A∩B)=P(B)*P(A) niebieskie to A∩B' czerwone to A∩B

a@b: To może tak: z rys Saizou ( schematu Venna) P(A∩B^')=P(A)−P(A∩B)

P(A∩B)		P(A)−P(A∩B)
	=
P(B)		1−P(B)

P(A∩B)−P(B)*P(A∩B)= P(A)*P(B)−P(B)*P(A∩B) P(A∩B)=P(A)*P(B) −−− zdarzenia A i B są niezależne