stereometria salamandra: Proszę o potwierdzenie zadań 5.1, 5.2, 5.4, jako że nie mam do nich odpowiedzi w książce 5.1. a) EFGH oraz ABCD ADEH oraz BCFG ABEF oraz DCHG b)ABEF, BCFG, DCHG, DAEH c) FG, BC, EH, AD d) skośne = prostopadłe (?) BF, CG, DH, AE 5.2. Tego nie wiem jak ruszyć 5.4. a) zakładając, że powstaje nam trójkąt DD₁B, to chodzi o kąt DBD₁ b) BD₁B₁ c) BD₁D Z góry dzięki

salamandra: https://i.imgur.com/cxQ2rPj.jpg

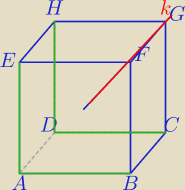
Mila: 5.1 d) krawędzie skośne to takie krawędzie nie leżą w jednej płaszczyźnie Przez FG i DC nie możesz poprowadzić płaszczyzny. Przez FG i AB FG i HD FG i AE Popatrz na krawędzie w pokoju −

salamandra: Te zielone które zaznaczyłaś to te skośne?

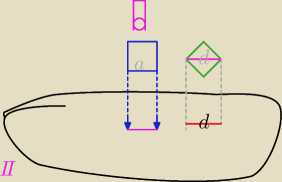
Mila: 5.2 Ustawiasz kartkę prostopadle do płaszczyzny π i oświetlasz z góry prostopadle do płaszczyzny π

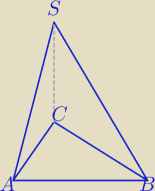
Mila: 5.1 Pary masz wypisane. Zielone, ale w stosunku do FG, a nie między sobą. Popatrz na krawędzie w pokoju. Nic Wam nauczyciel nie pokazywał na modelach? AB i SC są skośne , bo nie da się przez te krawędzie poprowadzić płaszczyzny. Wypisz inne pary.

salamandra: A w przypadku 5.1, FG i BF wyznaczą płaszczyznę, która jest ścianą BCFG tak? Jeśli tak, to już chyba pojmuję o co chodzi. W przypadku ostrosłupa, który podałaś − skośne: AB, SC CB, AS AC, SB?

Mila: Dobrze

salamandra: Tego 5.2 to nadal nie rozumiem, przez chwilę myślałem nawet, że zrobiłaś może inne zadanie

Mila: Ustaw kwadratową kartkę papieru prostopadle do blatu biurka i oświetlaj z góry latarką i obserwuj cień, to zrozumiesz.

salamandra: Zrobiłem ten eksperyment, cień się zmieniał w zależności od odległości światła, ale też od nachylenia (w moim przypadku pudełka po płycie cd), nie rozumiem polecenia tego zadania, naprowadziłabyś chociaż o jaki rzekomo odcinek w zadaniu chodzi?

Mila: Cień ma mieć długość boku kwadratu. Jeżeli kartkę ustawisz równolegle do blatu biurka to cień będzie miał kształt kwadratu gdy promienie światła mają padać prostopadle do blatu. Na rysunku nie widzisz bo jest w rzucie, musisz uruchomić wyobraźnię. Poszukam na youtubie.

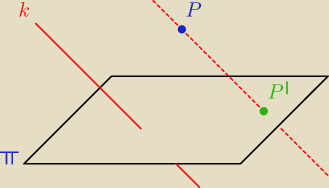
Saizou : Najpierw co to jest rzut równoległy? Niech dany będzie układ jak na rysunku (k− prosta wyznaczająca kierunek rzutu, P− punkt do zrzutowania, π − płaszczyzna na którą rzutujemy). W rzucie równoległym chodzi o to, żeby przez punkt P poprowadzić prostą równoległą do prostej k (wyznaczającej kierunek rzutu). Punkt przecięcia się tej prostej z płaszczyzną, to obraz punktu P w rzucie równoległym na płaszczyznę π. Najłatwiej jest wziąć prostą wyznaczającą kierunek, która jest prostopadła do płaszczyzny.

salamandra: Aha, czyli ten przedmiot (przykładowo to pudełko) muszę ułożyć równolegle do płaszczyzny (biurka)?

Saizou : Tak, ale tutaj chodzi o to, że jak będziesz zmieniać kąt padania światła, to zmieniać będzie się cień kwadratu.

salamandra: No właśnie, wiec kiedy ten odcinek (tak naprawdę nadal nie wiem co jest tym odcinkiem? Będzie równy bokowi kwadratu (tego przedmiotu rozumiem), a kiedy jego przekątna (domyślam się ze coś z 45 stopni pewnie trzeba kombinować?)

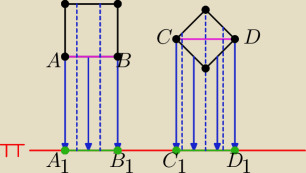
Saizou : Najłatwiej jest zrobić tak. kierunek rzutu prostopadły do płaszczyzny Pomyśl, czy rozumiesz rysunek

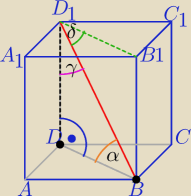
Mila: 5.4 α− kąt między przekątną BD₁ a płaszczyzną podstawy ABCD ( kąt między BD₁ i jej rzutem prostokątnym na pł. ABCD, BD jest rzutem) δ− kąt między przekątną BD₁ a płaszczyzną podstawy A₁B₁C₁D₁ γ − kąt między przekątną BD₁ i krawędzią boczną DD₁

salamandra: Dziękuję Milu, dzisiaj miałem konkretną już lekcję na temat tych kątów i rzutu prostokątnego, i już rozumiem

salamandra: Przynajmniej tak mi się wydaję, że rozumiem

Mila: Rozwiązuj zadania